Funcions trigonomètriques a 1r de BAT

Funcions trigonomètriques

En aquesta unitat estudiarem les funcions trigonomètriques.

Ja saps que la trigonometria ens permet relacionar els costats i els angles d'un triangle. Però amb les funcions trigonomètriques farem unes passes endavant, ens allunyarem dels triangles i veurem que les funcions trigonomètriques ens permetran modelitzar molts fenòmens de la natura, amb una especial atenció a aquells que són periòdics.

Marees
Ones de so.
Raigs de llum.
Òrbites dels planetes.
Cordes vibrants.
Pèndols.
Òrbites de les partícules atòmiques.

Abans de començar pots fer un repàs de:

Angles
Graus
Radians
Equivalència entre graus i radians
Línies trigonomètriques

Preparat per començar? Endavant, doncs: Funcions trigonomètriques !!!!!!!!!!!!!!!!

Funcions trigonomètriques

Funció sinus
- Característiques de la funció sinus
- Transformacions de la funció sinus
Funció cosinus
- Característiques de la funció cosinus
- Transformacions de la funció cosinus
Funció tangent
- Característiques de la funció tangent
Funcions inverses de les funcions trigonomètriques
- Repassar el concepte de Funció inversa
- La funció arc sinus
- La funció arc cosinus
- La funció arc tangent
Altres funcions trigonomètriques
Identitats i equacions trigonomètriques

Funció sinus

Anomenem funció sinus a la funció que a cada nombre real

x

li fa correspondre el valor del sinus de l'angle que mesura

x

radians, i l'expressem així:

f (x) = \sin x

Ara ens toca estudiar aquesta funció. Volem saber com és el seu gràfic i les seves principals característiques.

Podríem començar fent una taula de valors aprofitant les raons trigonomètriques dels principals angles que ja coneixem. Aquí la tens:

$(\cos x, \sin x)$	$x$ (en rad)	$f (x) = \sin (x)$
	$0$	$0$
	$\frac{π}{6} \approx 0.52$	$\frac{1}{2} = 0.5$
	$\frac{π}{4} \approx 0.79$	$\frac{\sqrt{2}}{2} \approx 0.71$
	$\frac{π}{3} \approx 1.05$	$\frac{\sqrt{3}}{2} \approx 0.87$
	$\frac{π}{2} \approx 1.57$	$1$
	$\frac{2 π}{3} \approx 2.09$	$\frac{\sqrt{3}}{2} \approx 0.87$
	$\frac{3 π}{4} \approx 2.36$	$\frac{\sqrt{2}}{2} \approx 0.71$
	$\frac{5 π}{6} \approx 2.62$	$\frac{1}{2} = 0.5$
	$π \approx 3.14$	$0$
	$\frac{7 π}{6} \approx 3.67$	$- \frac{1}{2} = - 0.5$
	$\frac{5 π}{4} \approx 3.93$	$- \frac{\sqrt{2}}{2} \approx - 0.71$
	$\frac{4 π}{3} \approx 4.19$	$- \frac{\sqrt{3}}{2} \approx - 0.87$
	$\frac{3 π}{2} \approx 4.71$	$- 1$
	$\frac{5 π}{3} \approx 5.24$	$- \frac{\sqrt{3}}{2} \approx - 0.87$
	$\frac{7 π}{4} \approx 5.5$	$- \frac{\sqrt{2}}{2} \approx - 0.71$
	$\frac{11 π}{6} \approx 5.76$	$- \frac{1}{2} = - 0.5$
	$2 π \approx 6.28$	$0$

I representant gràficament aquests punts tenim:

I, dibuixant la corba que passa per tots ells, obtenim:

També podem obtenir el gràfic amb l'ajuda del Geogebra:

Mou el punt de color blau (pots fer-ho clicant i arrossegant amb el ratolí) i observa què passa i mira d'entendre-ho.

Característiques de la funció sinus
Transformacions de la funció sinus

Característiques de la funció sinus

És important fixar-nos en que qualsevol valor de

x

té imatge, ja ho has pogut observar en el gràfic de Geogebra. Perquè donat qualsevol nombre real sempre hi ha un angle amb aquesta mesura (en rad, recordem), i aquest angle pot donar poques o moltes voltes, però segur que tindrà sinus. El que passarà és que els valors del sinus, molt sovint, apareixeran repetits.

Per exemple: com que $\frac{π}{6} + 2 π = \frac{13 π}{6}$ vol dir que els angles $\frac{13 π}{6}$ i $\frac{π}{6}$ són coterminals, és a dir, tenen el mateix costat final, només que $\frac{13 π}{6}$ ha donat una volta sencera i un tros final de $\frac{π}{6}$ . És per això que, tenint el mateix costat final, tindran el mateix sinus:

\sin \frac{13 π}{6} = \sin \frac{π}{6}

Passaria el mateix amb els infinits angles que obtindríem després de dues, tres, quatre, ... voltes senceres i un tros final de $\frac{π}{6}$ . També amb voltes negatives, és a dir, girant en sentit horari.

. . . = \sin (- \frac{23 π}{6}) = \sin (- \frac{11 π}{6}) = \sin \frac{π}{6} = \sin \frac{13 π}{6} = \sin \frac{25 π}{6} = . . .

Ho podem escriure així:

\sin \frac{π}{6} = \sin (\frac{π}{6} + 2 k π) \forall k \in ℤ

I el que passa amb

\frac{π}{6}

passa també amb qualsevol altre valor, per això, de forma general podem escriure:

\sin x = \sin (x + 2 k π) \begin{array}{c} \forall x \in ℝ \\ \forall k \in ℤ \end{array}

k

representa el nombre de voltes.

De manera informal podem dir que els valors del sinus es repeteixen cada $2 π$ . I de manera formal diem que:

f (x) = \sin (x)

és una funció periòdica i el seu període és

2 π

Observa i manipula la figura següent:

Anem ara a fixar-nos en els punts importants de la funció:

Els punts de tall amb l'eix OX es troben en els punts d'abscissa

. . ., - π, 0, π, 2 π, 3 π, 4 π, . . .

Les podem expressar totes de la forma següent:

k π \forall k \in ℤ

Els màxims es troben en els punts d'abscissa

. . ., \frac{π}{2}, \frac{5 π}{2}, \frac{9 π}{2}, . . .

Les podem expressar totes de la forma següent:

\frac{π}{2} + 2 k π \forall k \in ℤ

Els mínims es troben en els punts d'abscissa

. . ., - \frac{π}{2}, \frac{3 π}{2}, \frac{7 π}{2}, . . .

Les podem expressar totes de la forma següent:

\frac{3 π}{2} + 2 k π \forall k \in ℤ

Així que les característiques de la funció $f (x) = \sin (x)$ que ens interessa destacar ara són:

f (x) = \sin (x)

Domini: $ℝ$
Recorregut: $[- 1, 1]$
Funció contínua
Funció periòdica de període $2 π$
Funció simètrica respecte l'origen
Punts importants

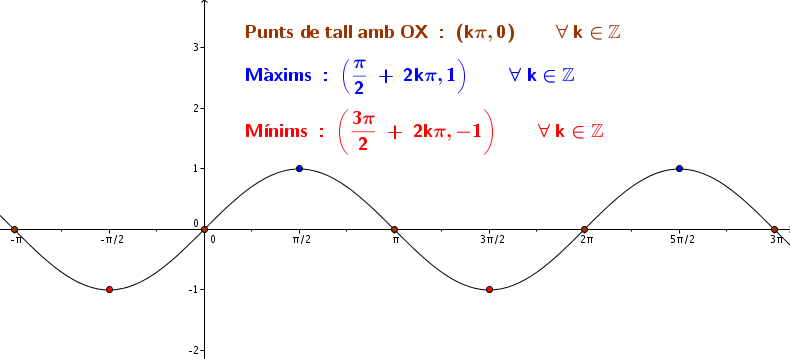
El gràfic de la funció sinus es coneix com sinusoide.

Transformacions de la funció sinus

La funció sinus molt sovint apareix combinada amb altres funcions (recorda les operacions amb funcions: multiplicar-les per un nombre, sumar-les, restar-les, multiplicar-les, dividir-les, i la composició de funcions)

Les noves funcions obtingudes fent alguna/es d'aquestes combinacions tenen gràfics relacionats amb el de la funció sinus, per això diem que són transformacions de la funció sinus.

Translació vertical
Dilatació-Contracció vertical
Translació horitzontal
Dilatació-Contracció horitzontal
Altres transformacions

En els apartats anteriors s'han estudiat per separat cadascuna d'aquestes transformacions, però molt sovint apareixen combinades algunes d'elles. Per exemple la funció $g (x) = 3 \sin (2 x + 1)$ .

De forma més general analitzarem funcions amb expressions de la forma:

g (x) = m \cdot \sin (n \cdot (x + k)) \forall m, n, k \in ℝ

Al gràfic següent pots modificar els valors de $k, m, n$ .

Translació vertical

Començarem amb funcions com

g (x) = \sin (x) + 4

que es pot interpretar com una suma

g (x) = f (x) + h (x)

, on

f (x) = \sin (x)

h (x) = 4

Només cal observar que la imatge de qualsevol $x_{0}$ per la funció $g (x)$ serà la de la funció $\sin (x)$ més 4 unitats.

Què provocarà aquest fet en el gràfic de la funció? Doncs, que el gràfic de $g (x)$ estarà format pels punts de $\sin (x)$ però desplaçats 4 unitats cap amunt.

De forma més general analitzarem funcions amb expressions de la forma:

g (x) = \sin x + k \forall k \in ℝ

Al gràfic següent pots modificar el valor de $k$ i moure el punt blau.

RECORDA

Podem obtenir el gràfic de $g (x) = \sin (x) + k$ a partir del de $f (x) = \sin (x)$ fent:

una translació vertical cap

\begin{array}{c} amunt si k > 0 \\ avall si k < 0 \end{array}

k

unitats.

Dilatació-Contracció vertical

Començarem amb funcions com

g (x) = 2 \sin x

que es pot interpretar com el producte d'una funció per una constant

g (x) = k \cdot f (x)

, on

f (x) = \sin (x)

k = 2

Només cal observar que la imatge de qualsevol $x_{0}$ per la funció $g (x)$ serà la de la funció $\sin (x)$ multiplicada per 2.

Què provocarà aquest fet en el gràfic de la funció? Doncs, que el gràfic de $g (x)$ estarà format pels punts de $\sin (x)$ però situats el doble de lluny de l'eix OX. Observa que els punts de tall amb l'eix OX no s'han mogut, perquè el doble de 0 és 0.

De forma més general analitzarem funcions amb expressions de la forma:

g (x) = k \cdot \sin x \forall k > 0

Al gràfic següent pots modificar el valor de $k$ i moure el punt blau $x_{0}$ .

RECORDA

Podem obtenir el gràfic de $g (x) = k \cdot \sin x$ a partir del de $f (x) = \sin (x)$ fent:

una dilatació (si

k > 1

) o contracció (si

0 < k < 1

) vertical de factor

k

Translació horitzontal

Començarem amb funcions com

g (x) = \sin (x + 2)

que es pot interpretar com una composició de funcions

g (x) = (f \circ h) (x) = f (h (x))

, on

f (x) = \sin (x)

h (x) = x + 2

Comprovem-ho:

g (x) = (f \circ h) (x) = f (h (x)) = f (x + 2) = \sin (x + 2)

Cal observar que la imatge de qualsevol $x_{0}$ per la funció $g (x)$ serà la de la funció $\sin (x)$ de $x_{0} + 2$ , és a dir del que està 2 unitats a la seva dreta.

Què provocarà aquest fet en el gràfic de la funció? Doncs, que el gràfic de $g (x)$ estarà format pels punts de $\sin (x)$ però desplaçats 2 unitats cap a l'esquerra.

De forma més general analitzarem funcions amb expressions de la forma:

g (x) = \sin (x + k) \forall k \in ℝ

Al gràfic següent pots modificar el valor de $k$ i moure el punt blau. Mira d'entendre perquè quan $k > 0$ és una translació cap a l'esquerra i quan $k < 0$ ho és cap a la dreta.

RECORDA

Podem obtenir el gràfic de $g (x) = \sin (x + k)$ a partir del de $f (x) = \sin (x)$ fent:

una translació horitzontal cap a

\begin{array}{c} l' esquerra si k > 0 \\ la dreta si k < 0 \end{array}

k

unitats.

Dilatació-Contracció horitzontal

Començarem amb funcions com

g (x) = \sin (2 x)

que es pot interpretar com la composició de dues funcions

g (x) = (f \circ h) (x) = f (h (x))

, on

f (x) = \sin (x)

h (x) = 2 x

Comprovem-ho:

g (x) = (f \circ h) (x) = f (h (x)) = f (2 x) = \sin (2 x)

Cal observar que la imatge de qualsevol $x_{0}$ per la funció $g (x)$ serà la de la funció $\sin (x)$ per a $2 x_{0}$ , és a dir, tindrà la imatge del que està el doble de lluny que ell de l'eix OY.

Què provocarà aquest fet en el gràfic de la funció? Doncs, que el gràfic de $g (x)$ estarà format pels punts de $\sin (x)$ però situats la meitat de lluny de l'eix OY. El punt de tall amb l'eix OY no s'ha mogut, perquè la meitat de 0 és 0.

De forma més general analitzarem funcions amb expressions de la forma:

g (x) = \sin (k x) \forall k > 0

Al gràfic següent pots modificar el valor de $k$ i moure el punt blau. Mira d'entendre perquè quan $k > 1$ és una contracció i quan $0 < k < 1$ és una dilatació, de factor $k$ . En aquests casos tenim la sinusoide però més atapeïda o més allargassada, canvia per tant el període, cosa que en les transformacions anteriors no passava. El període és ara $\frac{2 π}{k}$ .

RECORDA

Podem obtenir el gràfic de $g (x) = \sin (k x)$ a partir del de $f (x) = \sin (x)$ fent:

una contracció (si

k > 1

) o dilatació (si

0 < k < 1

) horitzontal de factor

k

El període de $g (x) = \sin (k x)$ és $\frac{2 π}{k}$ .

Altres transformacions

Començarem amb la funció

g (x) = - \sin (x)

És molt fàcil veure que la imatge de qualsevol $x_{0}$ per la funció $g (x)$ serà la de la funció $\sin (x)$ però canviada de signe.

Què provocarà aquest fet en el gràfic de la funció? Doncs, que el gràfic de $g (x)$ estarà format pels punts de $\sin (x)$ però situats simètricament respecte de l'eix OX. Els punts de tall amb l'eix OX no s'han mogut.

Al gràfic següent pots moure el punt blau $x_{0}$ .

RECORDA

Podem obtenir el gràfic de g(x) = -sin x a partir del de $f (x) = \sin (x)$ fent:

una reflexió respecte l'eix OX.

Continuarem amb la funció $g (x) = \sin (- x)$ .

És molt fàcil veure que la imatge de qualsevol $x_{0}$ per la funció $g (x)$ serà la de la funció $\sin (x)$ però de $- x_{0}$ . La imatge dels positius amb $g (x)$ serà la dels negatius amb $f (x) = \sin (x)$ i viceversa.

Què provocarà aquest fet en el gràfic de la funció? Doncs, que el gràfic de $g (x)$ estarà format pels punts de $\sin (x)$ però situats simètricament respecte de l'eix OY. El punt de tall amb l'eix OY no s'ha mogut.

Al gràfic següent pots moure el punt blau $x_{0}$ .

RECORDA

Podem obtenir el gràfic de $g (x) = \sin (- x)$ a partir del de $f (x) = \sin (x)$ fent:

una reflexió respecte l'eix OY.

Cal dir que, com has pogut observar, en el cas de la funció $f (x) = \sin (x)$ aquestes dues darreres transformacions han donat el mateix resultat. Però per motius diferents. Amb altres funcions (la funció cosinus, per exemple) es podrà veure que les dues transformacions porten a resultats diferents.

Per anar acabant, veurem la funció $g (x) = ∣ \sin (x) ∣$ . En aquest cas només posarem el gràfic. Analitzeu vosaltres què passa.

Finalment veurem la funció $g (x) = \sin ∣ x ∣$ . També posarem només el gràfic. Analitzeu vosaltres què passa.

En tots dos casos han desaparegut trossos de la funció vermella. Analitza què ha passat.

Funció cosinus

Anomenem funció cosinus a la funció que a cada nombre real

x

li fa correspondre el valor del cosinus de l'angle que mesura

x

radians, i l'expressem així:

f (x) = \cos x

Com en el cas de la funció sinus volem saber com és el seu gràfic i les seves principals característiques.

Comencem també fent una taula de valors aprofitant les raons trigonomètriques dels principals angles que ja coneixem. Aquí la tens:

$(\cos x, \sin x)$	$x$ (en rad)	$f (x) = \cos (x)$
	$0$	$1$
	$\frac{π}{6} \approx 0.52$	$\frac{\sqrt{3}}{2} \approx 0.87$
	$\frac{π}{4} \approx 0.79$	$\frac{\sqrt{2}}{2} \approx 0.71$
	$\frac{π}{3} \approx 1.05$	$\frac{1}{2} = 0.5$
	$\frac{π}{2} \approx 1.57$	$0$
	$\frac{2 π}{3} \approx 2.09$	$- \frac{1}{2} = - 0.5$
	$\frac{3 π}{4} \approx 2.36$	$- \frac{\sqrt{2}}{2} \approx - 0.71$
	$\frac{5 π}{6} \approx 2.62$	$- \frac{\sqrt{3}}{2} \approx - 0.87$
	$π \approx 3.14$	$- 1$
	$\frac{7 π}{6} \approx 3.67$	$- \frac{\sqrt{3}}{2} \approx - 0.87$
	$\frac{5 π}{4} \approx 3.93$	$- \frac{\sqrt{2}}{2} \approx - 0.71$
	$\frac{4 π}{3} \approx 4.19$	$- \frac{1}{2} = - 0.5$
	$\frac{3 π}{2} \approx 4.71$	$- 1$
	$\frac{5 π}{3} \approx 5.24$	$\frac{1}{2} = 0.5$
	$\frac{7 π}{4} \approx 5.5$	$\frac{\sqrt{2}}{2} \approx 0.71$
	$\frac{11 π}{6} \approx 5.76$	$\frac{\sqrt{3}}{2} \approx 0.87$
	$2 π \approx 6.28$	$1$

I representant gràficament aquests punts tenim:

Posar l'exercici "Punts del cosinus", encara per fer!!!!

I, dibuixant la corba que passa per tots ells, obtenim:

També podem obtenir el gràfic amb l'ajuda del Geogebra:

Mou el punt de color blau (pots fer-ho clicant i arrossegant amb el ratolí) i observa què passa i mira d'entendre-ho.

Característiques de la funció cosinus
Transformacions de la funció cosinus

Transformacions de la funció cosinus

Les transformacions aplicades a la funció sinus tenen exactament el mateix comportament amb el cosinus. Així que només cal que practiquis.

g (x) = A \cdot \cos (B \cdot (x + C)) + D \forall A, B, C, D \in ℝ

Al gràfic següent pots modificar els valors de $A, B, C, D$ .

Característiques de la funció cosinus

Les consideracions que hem fet amb la funció sinus pel que fa al domini i la periodicitat són també aplicables a la funció cosinus.

\cos x = \cos (x + 2 k π) \begin{array}{c} \forall x \in ℝ \\ \forall k \in ℤ \end{array}

k

representa el nombre de voltes.

$f (x) = \cos (x)$ és una funció periòdica i el seu període és $2 π$ .

Sí que hem de fixar-nos en els punts importants de la funció cosinus:

Els punts de tall amb l'eix OX es troben en els punts d'abscissa

. . ., - \frac{π}{2}, \frac{π}{2}, \frac{3 π}{2}, \frac{5 π}{2}, \frac{7 π}{2}, \frac{9 π}{2}, . . .

Les podem expressar totes de la forma següent:

\frac{π}{2} + k π \forall k \in ℤ

Els màxims es troben en els punts d'abscissa

. . ., - 2 π, 0, 2 π, 4 π, . . .

Les podem expressar totes de la forma següent:

2 k π \forall k \in ℤ

Els mínims es troben en els punts d'abscissa

. . ., - π, π, 3 π, 5 π . . .

Les podem expressar totes de la forma següent:

(2 k + 1) π \forall k \in ℤ

Així que les característiques de la funció $f (x) = \cos (x)$ que ens interessa destacar ara són:

f (x) = \cos (x)

Domini:
Recorregut: $[- 1, 1]$
Funció contínua
Funció periòdica de període $2 π$
Funció simètrica respecte l'eix d'ordenades
Punts importants

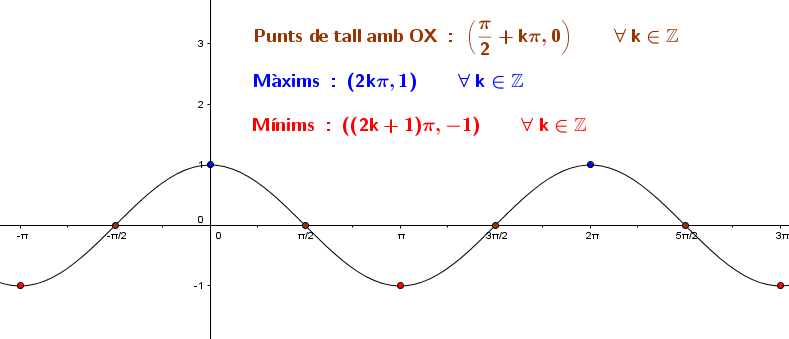
Funció tangent

Anomenem funció tangent a la funció que a cada nombre real

x

li fa correspondre el valor de la tangent de l'angle que mesura

x

radians, i l'expressem així:

f (x) = \tan x

o també

f (x) = tg x

Com en el cas de la funció sinus i cosinus volem saber com és el seu gràfic i les seves principals característiques.

Comencem també fent una taula de valors aprofitant les raons trigonomètriques dels principals angles que ja coneixem. Aquí la tens:

$(\cos x, \sin x)$ $\tan x = \frac{\sin x}{\cos x}$	$x$ (en rad)	$f (x) = \tan (x)$
	$0$	$0$
	$\frac{π}{6} \approx 0.52$	$\frac{\sqrt{3}}{3} \approx 0.58$
	$\frac{π}{4} \approx 0.79$	$1$
	$\frac{π}{3} \approx 1.05$	$\sqrt{3} \approx 1.73$
	$\frac{π}{2} \approx 1.57$	$∄$
	$\frac{2 π}{3} \approx 2.09$	$- \sqrt{3} \approx - 1.73$
	$\frac{3 π}{4} \approx 2.36$	$- 1$
	$\frac{5 π}{6} \approx 2.62$	$- \frac{\sqrt{3}}{3} \approx - 0.58$
	$π \approx 3.14$	$0$
	$\frac{7 π}{6} \approx 3.67$	$\frac{\sqrt{3}}{3} \approx 0.58$
	$\frac{5 π}{4} \approx 3.93$	$1$
	$\frac{4 π}{3} \approx 4.19$	$\sqrt{3} \approx 1.73$
	$\frac{3 π}{2} \approx 4.71$	$∄$
	$\frac{5 π}{3} \approx 5.24$	$- \sqrt{3} \approx - 1.73$
	$\frac{7 π}{4} \approx 5.5$	$- 1$
	$\frac{11 π}{6} \approx 5.76$	$- \frac{\sqrt{3}}{3} \approx - 0.58$
	$2 π \approx 6.28$	$0$

A destacar que, a diferència de les funcions sinus i cosinus, la funció tangent no assigna imatge a tots els nombres reals. Veiem a la taula que $\frac{π}{2}$ i $\frac{3 π}{2}$ no tenen imatge. De fet, hi haurà infinits nombres com aquests. Tots els de la forma $\frac{π}{2} + k π, \forall k \in ℤ$ . Això suposarà un gran canvi en el gràfic d'aquesta funció.

Provem de representar gràficament aquests punts:

Posar l'exercici "Punts del cosinus", encara per fer!!!!

Ara és molt perillós fer passar una línia per tots aquests punts perquè ja hem vist que $\frac{π}{2} \approx 1.57$ i $\frac{3 π}{2} \approx 4.71$ no tenen imatge i per tant aquesta funció no pot ser contínua. En aquest cas ens va molt bé el Geogebra perquè amb ell situarem una "infinitat" de punts i podrem veure molt bé com és el gràfic de la funció tangent.

Mou el punt de color blau $x_{0}$ (pots fer-ho clicant i arrossegant amb el ratolí) i observa què passa i mira d'entendre-ho. Ja te n'hauràs adonat que les discontinuïtats són asimptòtiques. De fet, en té infinites d'asímptotes. A continuació en pots veure unes quantes.

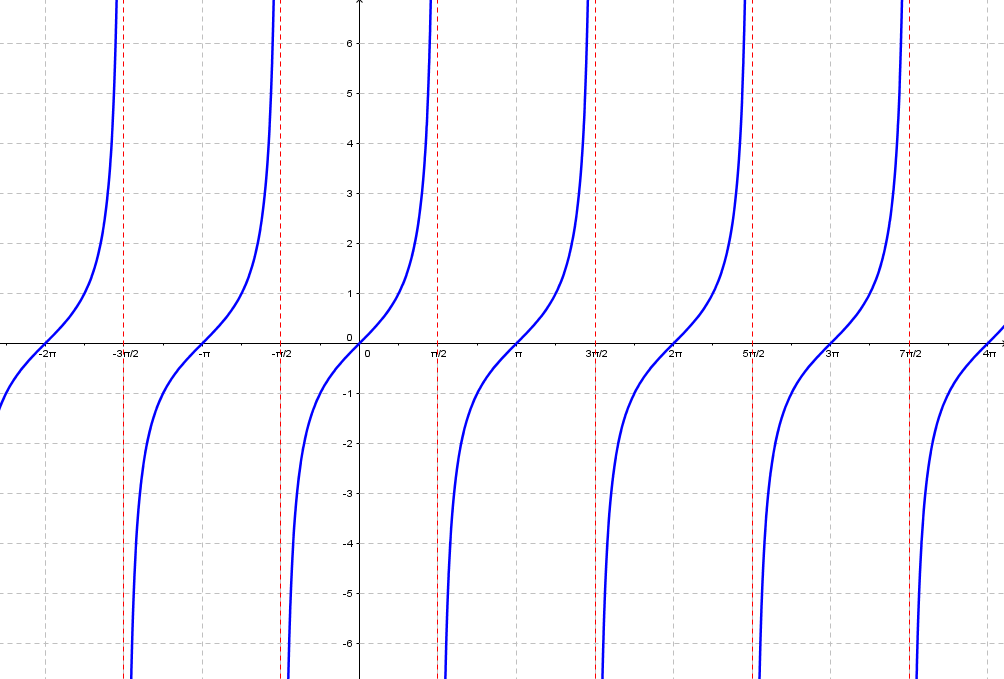
Característiques de la funció tangent

Característiques de la funció tangent

Ja hem comentat a l'apartat anterior que, a diferència de les funcions sinus i cosinus, la funció tangent no assigna imatge a tots els nombres reals,

\frac{π}{2}

\frac{3 π}{2}

no tenen imatge, i n'hi haurà infinits de nombres com aquests. Tots els de la forma

\frac{π}{2} + k π, \forall k \in ℤ

. Així que mentre el domini de les funcions sinus i cosinus era

ℝ

, ara el domini de la tangent serà:

D_{f} = ℝ \sim {\frac{π}{2} + k π}, \forall k \in ℤ

El que passarà també és que els valors de la tangent apareixeran repetits. Però es repetiran amb amb un període diferent.

Per exemple:

\tan \frac{7 π}{6} = \tan \frac{π}{6}

Ara es repeteixen cada mitja volta, és a dir cada $π$ rad.

. . . = \tan (- \frac{11 π}{6}) = \tan (- \frac{5 π}{6}) = \tan \frac{π}{6} = \tan \frac{7 π}{6} = \tan \frac{13 π}{6} = . . .

Ho podem escriure així:

\tan \frac{π}{6} = \tan (\frac{π}{6} + k π), \forall k \in ℤ

I el que passa amb

\frac{π}{6}

passa també amb qualsevol altre valor, per això, de forma general podem escriure:

\tan x = \tan (x + k π) \begin{array}{c} \forall x \in ℝ \\ \forall k \in ℤ \end{array}

k

representa el nombre de mitges voltes.

De manera informal podem dir que els valors de la tangent es repeteixen cada $π$ . I de manera formal diem que:

f (x) = \tan (x)

és una funció periòdica i el seu període és

π

Observa i manipula la figura següent:

Anem ara a fixar-nos en els punts importants, que ara seran només punts de tall amb l'eix OX i discontinuïtats de la funció. És prou evident que no té màxims ni mínims.

Els punts de tall amb l'eix OX es troben en els punts d'abscissa

. . ., - 2 π, - π, 0, π, 2 π, 3 π, . . .

Les podem expressar totes de la forma següent:

k π \forall k \in ℤ

Les discontinuïtats es troben en els punts d'abscissa

. . ., - \frac{3 π}{2}, - \frac{π}{2}, \frac{π}{2}, \frac{3 π}{2}, \frac{5 π}{2}, . . .

Les podem expressar totes de la forma següent:

\frac{π}{2} + k π \forall k \in ℤ

Ja hem dit que les discontinuïtats són asimptòtiques i per tant la funció tangent té infinites asímptotes verticals d'equacions:

x = \frac{π}{2} + k π \forall k \in ℤ

Així que les característiques de la funció $f (x) = \tan (x)$ que ens interessa destacar ara són:

f (x) = \tan (x)

Domini: $ℝ \sim {\frac{π}{2} + k π}, \forall k \in ℤ$
Recorregut: $ℝ$
Funció creixent
Té infinites discontinuïtats asimptòtiques
Funció periòdica de període $π$
Funció simètrica respecte l'origen
Punts importants

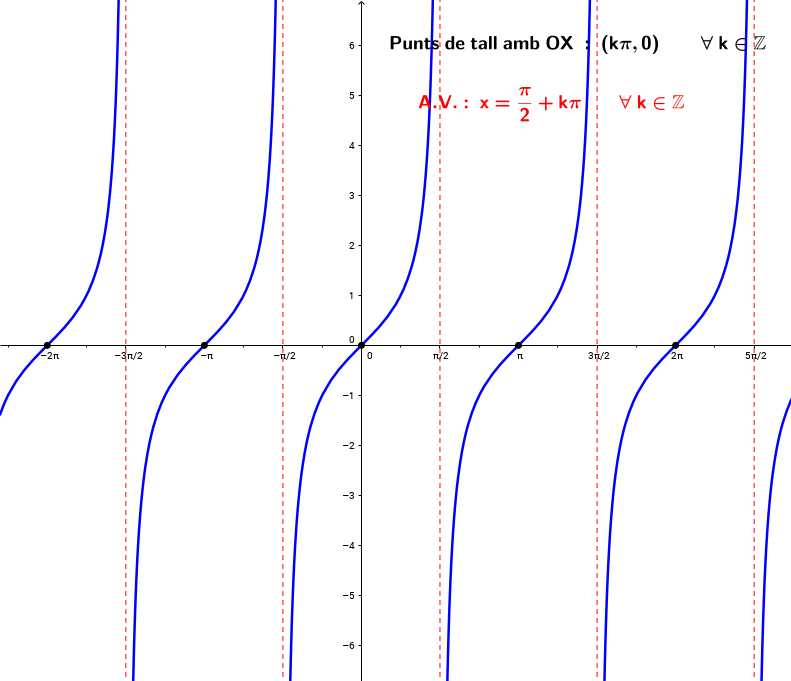
Les discontinuïtats asimptòtiques les haguéssim pogut estudiar com fèiem en el tema de límits i continuïtat, analitzem per exemple en $x = \frac{π}{2}$ :

$f (\frac{π}{2}) = \tan (\frac{π}{2}) = \frac{\sin (\frac{π}{2})}{\cos (\frac{π}{2})} = \frac{1}{0} = ∄$
$\lim_{x \to \frac{π}{2}} f (x) = \lim_{x \to \frac{π}{2}} \tan x = \lim_{x \to \frac{π}{2}} \frac{\sin x}{\cos x} = \frac{\sin (\frac{π}{2})}{\cos (\frac{π}{2})} = \frac{1}{0} = ∞$
I, per tant, caldria fer límits laterals per tenir més informació de l'asímptota.
- per l'esquera: $\lim_{x \to {\frac{π}{2}}^{-}} f (x) = \lim_{x \to {\frac{π}{2}}^{-}} \tan x = \lim_{x \to {\frac{π}{2}}^{-}} \frac{\sin x}{\cos x} = \frac{\sin ({\frac{π}{2}}^{-})}{\cos ({\frac{π}{2}}^{-})} = \frac{1}{0^{+}} = + ∞$
- per la dreta: $\lim_{x \to {\frac{π}{2}}^{+}} f (x) = \lim_{x \to {\frac{π}{2}}^{+}} \tan x = \lim_{x \to {\frac{π}{2}}^{+}} \frac{\sin x}{\cos x} = \frac{\sin ({\frac{π}{2}}^{+})}{\cos ({\frac{π}{2}}^{+})} = \frac{1}{0^{-}} = - ∞$

Funcions inverses de les funcions trigonomètriques

Pot ser cal que repassis el concepte de Funció inversa .

La funció arc sinus
La funció arc cosinus
La funció arc tangent

Funció inversa

Donada una funció

f

, la funció inversa de

f

és una altra funció, que representem per

f^{- 1}

, que desfà l'acció que ha fet

f

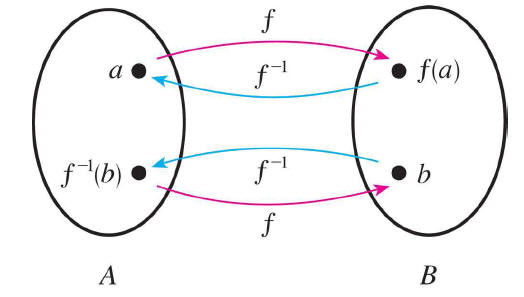
Per exemple, si tenim una funció $f$ que al 3 li assigna el 8, la seva funció inversa $f^{- 1}$ al 8 li assignarà el 3, Dit d'una altra manera, si la funció $f$ passa pel punt $(3, 8)$ , la seva funció inversa $f^{- 1}$ passarà pel punt $(8, 3)$ .

També, si tenim una funció $f$ que assigna imatges multiplicant per 3, és a dir, $f (x) = 3 x$ , la seva funció inversa $f^{- 1}$ assignarà imatges dividint per 3, és a dir, $f^{- 1} (x) = \frac{x}{3}$ .

Concretant, això vol dir que si la imatge de 5 per $f$ és 15, la imatge de 15 per $f^{- 1}$ ha de ser 5. Expressant-ho formalment:

f (5) = 3 \cdot 5 = 15

f^{- 1} (15) = \frac{15}{3} = 5

Dit d'una altra manera, quan actua una funció darrera de l'altra (recorda: això és una composició de funcions) sobre el 5 obtenim el mateix 5.

(f^{- 1} \circ f) (5) = f^{- 1} (f (5)) = f^{- 1} (15) = 5

També:

(f \circ f^{- 1}) (15) = f (f^{- 1} (15)) = f (5) = 15

I això s'ha de complir no només per al 5 sinó per a qualsevol nombre real $x \in ℝ$ .

(f^{- 1} \circ f) (x) = f^{- 1} (f (x)) = f^{- 1} (3 x) = \frac{3 x}{3} = x

També:

(f \circ f^{- 1}) (x) = f (f^{- 1} (x)) = f (\frac{x}{3}) = 3 \cdot \frac{x}{3} = x

DEFINICIÓ

Diem que una funció $f^{- 1}$ és la inversa d'una altra $f$ quan es compleixen:

$(f^{- 1} \circ f) (x) = x$
$(f \circ f^{- 1}) (x) = x$

Cal tenir en compte que hi ha funcions que no tenen inversa. I que si una funció $f$ té inversa, la inversa d'aquesta inversa és la mateixa $f$ . Ès a dir: ${(f^{- 1})}^{- 1} = f$ .

Càlcul de la funció inversa
Gràfic de la funció inversa
Quines funcions no tenen inversa?

Càlcul de la funció inversa

En els casos més senzills podem trobar la funció inversa directament.

EXEMPLE

Troba la funció inversa de $f (x) = 6 x$ . Després comprova que $(f^{- 1} \circ f) (x) = x$ i $(f \circ f^{- 1}) (x) = x$ .

Solució

Exercici: Càlcul de la funció inversa - I

Pot ser que ens interessi comprovar si una funció és inversa d'una altra.

EXEMPLE

Quina de les funcions $g (x)$ o $h (x)$ és la funció inversa de $f (x) = \frac{5}{x - 2}$ .

g (x) = \frac{x - 2}{5} h (x) = \frac{5}{x} + 2

Solució

Quan l'expressió de la funció $f$ és més complexa, no és tan fàcil trobar l'expressió de la inversa. En aquests casos podem seguir els següents passos:

Igualar l'expressió de la funció $f (x)$ a $y$ .
Aïllar la $x$ a la igualtat anterior.
Canviar $x$ per $y$ i viceversa.

EXEMPLE

Troba la inversa de la funció $f (x) = \frac{}{}$ .

Solució

Si ens demanen que després de trobar la funció inversa comprovem que ho és, hem de comprovar, tal com hem fet als dos primers exemples, que:

(f^{- 1} \circ f) (x) = x

(f \circ f^{- 1}) (x) = x

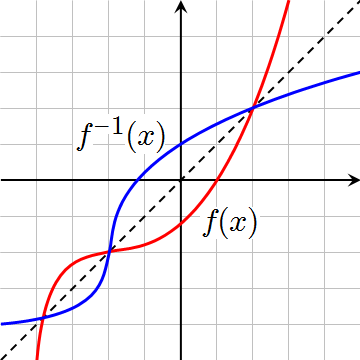
Gràfic de la funció inversa

Ara ens interessa veure quina relació hi ha entre el gràfic d'aquestes dues funcions,

f

f^{- 1}

. Començarem dient que si

f

passa pel punt

(5, 15)

, llavors

f^{- 1}

passa pel punt

(15, 5)

. És a dir, el punt amb les mateixes coordenades però canviades d'ordre. I això què suposarà pel que fa al gràfic?

En el gràfic següent s'ha construït un punt B amb les mateixes coordenades que un altre A però canviades de lloc. Mou el punt blau A i te n'adonaràs quina relació hi ha.

Així, doncs, podem dir que els gràfics de les funcions $f$ i $f^{- 1}$ són simètrics respecte de la bisectriu del primer i tercer quadrants (la recta d'equació $y = x$ ).

Quines funcions no tenen inversa?

Ja hem dit que no totes les funcions tenen inversa. Però, quines són les que no en tenen?

Doncs aquelles que tenen algun/s valor/s de la variable dependent amb més d'una antiimatge. Perquè la seva inversa assignaria a aquest valor més d'una imatge i recordem que les funcions a cada valor de la variable independent els hi assignen un ÚNIC valor de la variable dependent.

Això ho podem veure en qualsevol de les formes en que pot venir donada una funció. En forma de taula.

$x$	-1	2	3	5	8	9
$f (x)$	3	-5	1	3	2	0

Observa que el 3 té dues antiimatges, el -1 i el 5. Llavors $f^{- 1}$ li assignaria, al 3, dues imatges i per tant no seria funció. Diem que $f$ no té inversa, $∄ f^{- 1}$ . El mateix passa en les següents situacions:

$g (x) = {(1, 9), (2, 13), (3, 15), (4, 15), (5, 12), (6, 10)}$
$∄ g^{- 1}$	$∄ h^{- 1}$

Són especialment interessants els casos en que la funció ens la donen en forma de gràfic o de fórmula. Els analitzem conjuntament.

Donada la funció $f (x) = x^{2}$ . En intentar trobar la inversa fem: $y = x^{2} \to x = \pm \sqrt{y} \to y = \pm \sqrt{x}$ i això ja ens indica que $∄ f^{- 1}$ , qualsevol $x \in ℝ^{+}$ tindria dues imatges i això no pot ser.

Analitzem-ho ara gràficament. Saps molt bé que el gràfic de la funció $f (x) = x^{2}$ és la paràbola següent, i el gràfic de la inversa hauria de ser el que veus, però ... clar, no seria funció!!

La idea és la següent: si es pot dibuixar alguna línia recta horitzontal que talli el gràfic de la funció $f$ en més d'un punt, llavors la funció $f$ no té inversa. És a dir, $∄ f^{- 1}$ .

Dit d'una altra manera, si totes les línies rectes horitzontals que es poden dibuixar tallen el gràfic de la funció $f$ com a màxim en un punt, llavors la funció $f$ té inversa. És a dir, $\exists f^{- 1}$ .

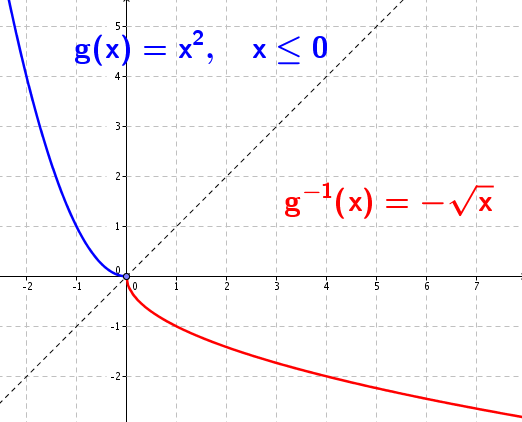
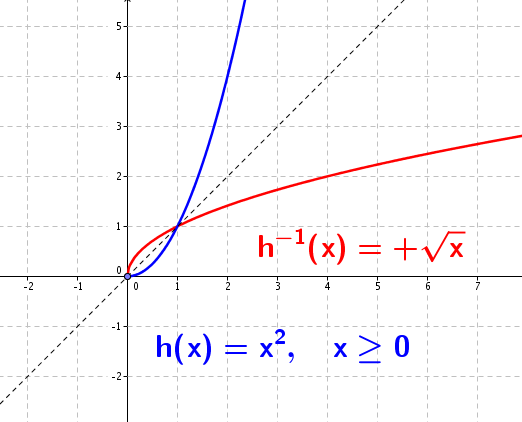
Però les funcions que no tenen inversa podem desfer-les en trossos de manera adequada per tal que en cada tros sí que tinguin inversa. I, com ho fem això de fer trossos d'una funció? Doncs, restringint el domini. Agafant una part només del domini inicial de la funció. És per això que aquestes inverses s'anomenen inversa parcial o inversa local .

En el cas de la funció anterior $f (x) = x^{2}$ faríem el següent:


$\exists g^{- 1}$	$\exists h^{- 1}$

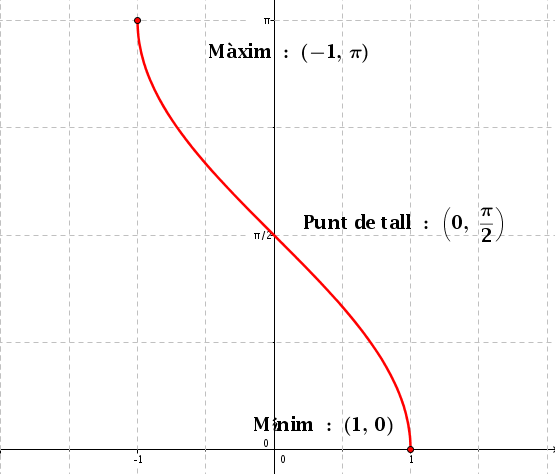
La funció arc cosinus

La funció arc cosinus és la funció inversa de la funció cosinus. És a dir:

f (x) = \cos (x) ⟶ f^{- 1} (x) = \arccos (x)

$f (x) = \arccos (x) ⟶ f^{- 1} (x) = \cos (x)$

$\cos^{- 1} (x) = \arccos (x)$

$\arccos^{- 1} (x) = \cos (x)$

Són diferents maneres d'expressar aquesta idea. Aprofitem per dir que moltes calculadores utilitzen l'expressió $\cos^{- 1}$ , i molts programes d'ordinador $acos (x)$ .

Però, pot ser hem anat massa de pressa!!! Primer ens hauríem d'haver plantejat si la funció cosinus té inversa!!!!

Ja deus haver observat que no en té, és de les que té inversa local o inversa parcial, són les que hem de restringir el domini per tal que tinguin inversa.

Arrossega el punt A, en el gràfic següent, i te n'adonaràs que el gràfic simètric de la funció $f (x) = \cos (x)$ respecte la recta $y = x$ no correspondria a una funció.

Per tant, cal fer una restricció en el domini de la funció cosinus per tal que això no passi.

Ens quedem amb el tros $0 \leq x \leq π = [0, π]$

Si haguéssim fet taula de valors tindríem:

$x$	$f (x) = \arccos (x)$
$- 1$	$π \approx 3.14$
$- \frac{\sqrt{3}}{2} \approx - 0.87$	$\frac{5 π}{6} \approx 2.62$
$- \frac{\sqrt{2}}{2} \approx - 0.71$	$\frac{3 π}{4} \approx 2.36$
$- \frac{1}{2} = - 0.5$	$\frac{2 π}{3} \approx 2.09$
$0$	$\frac{π}{2} \approx 1.57$
$\frac{1}{2} = 0.5$	$\frac{π}{3} \approx 1.05$
$\frac{\sqrt{2}}{2} \approx 0.71$	$\frac{π}{4} \approx 0.79$
$\frac{\sqrt{3}}{2} \approx 0.87$	$\frac{π}{6} \approx 0.52$
$1$	$0$

Finalment podem fer un recull de les característiques d'aquesta funció.

f (x) = \arccos (x)

Domini: [-1, 1]
Recorregut: $[0, π]$
És una funció contínua
És una funció decreixent
Punts importants

La funció arc tangent

La funció arc tangent és la funció inversa de la funció tangent. És a dir:

f (x) = \tan (x) ⟶ f^{- 1} (x) = \arctan (x)

$f (x) = \arctan (x) ⟶ f^{- 1} (x) = \tan (x)$

$\tan^{- 1} (x) = \arctan (x)$

$\arctan^{- 1} (x) = \tan (x)$

Són diferents maneres d'expressar aquesta idea. Aprofitem per dir que moltes calculadores utilitzen l'expressió $\tan^{- 1}$ , i molts programes d'ordinador $atan (x)$ .

Però, pot ser hem anat massa de pressa!!! Primer ens hauríem d'haver plantejat si la funció tangent té inversa!!!!

Ja deus haver observat que no en té, és de les que té inversa local o inversa parcial, són les que hem de restringir el domini per tal que tinguin inversa.

Arrossega el punt X, en el gràfic següent, i te n'adonaràs que el gràfic simètric de la funció $f (x) = \tan (x)$ respecte la recta $y = x$ no correspondria a una funció.

Per tant, cal fer una restricció en el domini de la funció tangent per tal que això no passi.

Ens quedem amb el tros $- \frac{π}{2} < x < \frac{π}{2} = (- \frac{π}{2}, \frac{π}{2})$

Si haguéssim fet taula de valors tindríem:

$x$	$f (x) = \arctan (x)$
$- \sqrt{3} \approx - 1.73$	$- \frac{π}{3} \approx - 1.05$
$- 1$	$- \frac{π}{4} \approx - 0.79$
$- \frac{\sqrt{3}}{3} \approx - 0.58$	$- \frac{π}{6} \approx - 0.52$
$0$	$0$
$\frac{\sqrt{3}}{3} \approx 0.58$	$\frac{π}{6} \approx 0.52$
$1$	$\frac{π}{4} \approx 0.79$
$\sqrt{3} \approx 1.73$	$\frac{π}{3} \approx 1.05$

Finalment podem fer un recull de les característiques d'aquesta funció.

f (x) = \arctan (x)

Domini: $(- ∞, + ∞) = ℝ$
Recorregut: $(- \frac{π}{2}, \frac{π}{2})$
És una funció contínua
És una funció creixent
Punts importants

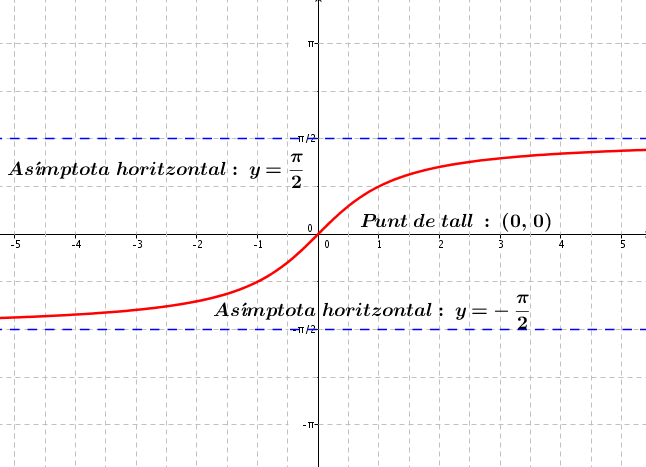
Fixa't que aquestes assímptotes horitzontals ens indiquen:

$\lim_{x \to - ∞} f (x) = \lim_{x \to - ∞} \arctan x = - \frac{π}{2}$
$\lim_{x \to + ∞} f (x) = \lim_{x \to + ∞} \arctan x = \frac{π}{2}$

La funció arc sinus

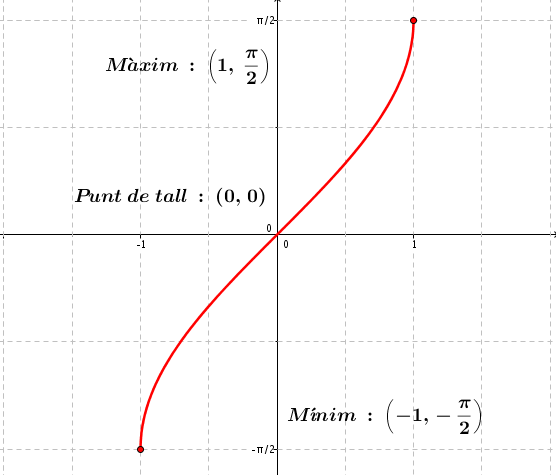
La funció arc sinus és la funció inversa de la funció sinus. És a dir:

f (x) = \sin (x) ⟶ f^{- 1} (x) = \arcsin (x)

$f (x) = \arcsin (x) ⟶ f^{- 1} (x) = \sin (x)$

$\sin^{- 1} (x) = \arcsin (x)$

$\arcsin^{- 1} (x) = \sin (x)$

Són diferents maneres d'expressar aquesta idea. Aprofitem per dir que moltes calculadores utilitzen l'expressió $\sin^{- 1}$ , i molts programes d'ordinador $asin (x)$ .

Però, pot ser hem anat massa de pressa!!! Primer ens hauríem d'haver plantejat si la funció sinus té inversa!!!!

Ja deus haver observat que no en té, és de les que té inversa local, són les que hem de restringir el domini per tal que tinguin inversa.

Arrossega el punt A, en el gràfic següent, i te n'adonaràs que el gràfic simètric de la funció $f (x) = \sin (x)$ respecte la recta $y = x$ no correspondria a una funció.

Per tant, cal fer una restricció en el domini de la funció sinus per tal que això no passi. Ens quedem amb el tros $- \frac{π}{2} \leq x \leq \frac{π}{2}$

Si haguéssim fet taula de valors tindríem:

$x$	$f (x) = \arcsin (x)$
$- 1$	$- \frac{π}{2} \approx - 1.57$
$- \frac{\sqrt{3}}{2} \approx - 0.87$	$- \frac{π}{3} \approx - 1.05$
$- \frac{\sqrt{2}}{2} \approx - 0.71$	$- \frac{π}{4} \approx - 0.79$
$- \frac{1}{2} = - 0.5$	$- \frac{π}{6} \approx - 0.52$
$0$	$0$
$\frac{1}{2} = 0.5$	$\frac{π}{6} \approx 0.52$
$\frac{\sqrt{2}}{2} \approx 0.71$	$\frac{π}{4} \approx 0.79$
$\frac{\sqrt{3}}{2} \approx 0.87$	$\frac{π}{3} \approx 1.05$
$1$	$\frac{π}{2} \approx 1.57$

Finalment podem fer un recull de les característiques d'aquesta funció.

f (x) = \arcsin (x)

Domini: [-1, 1]
Recorregut: $[- \frac{π}{2}, \frac{π}{2}]$
És una funció contínua
És una funció creixent
Punts importants

Cotangent

Recorda que $\cot α = \frac{1}{\tan α} = \frac{\cos α}{\sin α}$

Anomenem funció cotangent a la funció que a cada nombre real

x

li fa correspondre el valor de la cotangent de l'angle que mesura

x

radians, i l'expressem així:

f (x) = \cot x

També volem saber com és el seu gràfic i les seves principals característiques.

Comencem també fent una taula de valors aprofitant les raons trigonomètriques dels principals angles que ja coneixem. Aquí la tens:

$(\cos x, \sin x)$ $\cot x = \frac{\cos x}{\sin x}$	$x$ (en rad)	$f (x) = \cot (x)$
	$0$	$∄$
	$\frac{π}{6} \approx 0.52$	$\sqrt{3} \approx 1.73$
	$\frac{π}{4} \approx 0.79$	$1$
	$\frac{π}{3} \approx 1.05$	$\frac{\sqrt{3}}{3} \approx 0.58$
	$\frac{π}{2} \approx 1.57$	$0$
	$\frac{2 π}{3} \approx 2.09$	$- \frac{\sqrt{3}}{3} \approx - 0.58$
	$\frac{3 π}{4} \approx 2.36$	$- 1$
	$\frac{5 π}{6} \approx 2.62$	$- \sqrt{3} \approx - 1.73$
	$π \approx 3.14$	$∄$
	$\frac{7 π}{6} \approx 3.67$	$\sqrt{3} \approx 1.73$
	$\frac{5 π}{4} \approx 3.93$	$1$
	$\frac{4 π}{3} \approx 4.19$	$\frac{\sqrt{3}}{3} \approx 0.58$
	$\frac{3 π}{2} \approx 4.71$	$0$
	$\frac{5 π}{3} \approx 5.24$	$- \frac{\sqrt{3}}{3} \approx - 0.58$
	$\frac{7 π}{4} \approx 5.5$	$- 1$
	$\frac{11 π}{6} \approx 5.76$	$- \sqrt{3} \approx - 1.73$
	$2 π \approx 6.28$	$∄$

Com la funció tangent, la funció cotangent no assigna imatge a tots els nombres reals. Veiem a la taula que $0$ , $π$ i $2 π$ no tenen imatge. De fet, hi haurà infinits nombres com aquests. Tots els de la forma $k π, \forall k \in ℤ$ . Això suposarà que aquesta funció també tindrà discontinuïtats.

Provem de representar gràficament aquests punts:

Posar l'exercici "Punts del cosinus", encara per fer!!!!

Ara és molt perillós fer passar una línia per tots aquests punts perquè ja hem vist que $0$ , $π$ i $2 π$ no tenen imatge i per tant aquesta funció no pot ser contínua. En aquest cas ens va molt bé el Geogebra perquè amb ell situarem una "infinitat" de punts i podrem veure molt bé com és el gràfic de la funció cotangent.

Mou el punt de color blau $x_{0}$ (pots fer-ho clicant i arrossegant amb el ratolí o amb les tecles del cursor) i observa què passa i mira d'entendre-ho. Ja te n'hauràs adonat que les discontinuïtats són asimptòtiques. De fet, en té infinites d'asímptotes.

Així que les característiques de la funció $f (x) = \cot (x)$ que ens interessa destacar ara són:

f (x) = \cot (x)

Domini: $ℝ \sim {k π}, \forall k \in ℤ$
Recorregut: $ℝ$
Funció decreixent
Té infinites discontinuïtats asimptòtiques
Funció periòdica de període $π$
És simètrica respecte l'origen
Punts importants

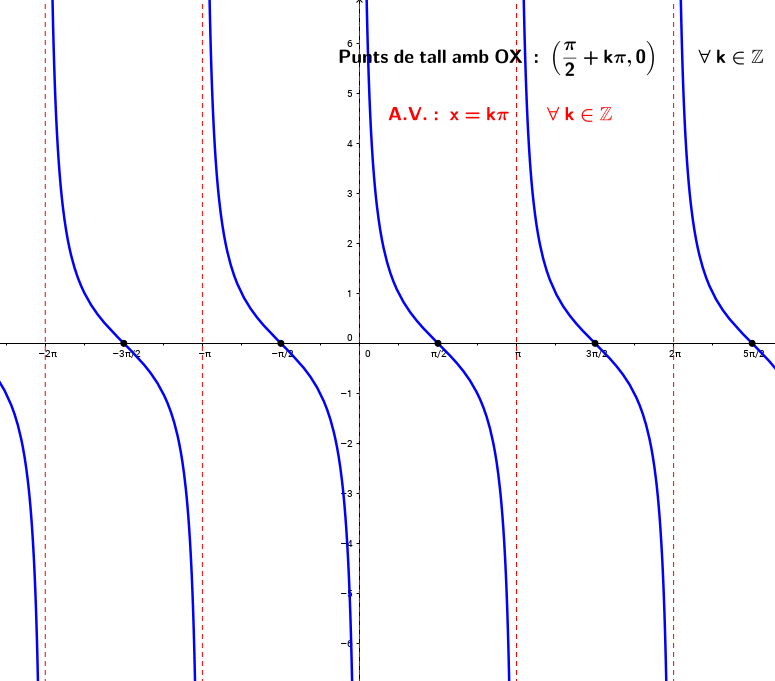
És important que miris conjuntament els gràfics de les funcions $\tan x$ i $\cot x$ . Observa que en els punts de tall amb l'eix OX d'una és on hi té les asímptotes verticals l'altra i viceversa.

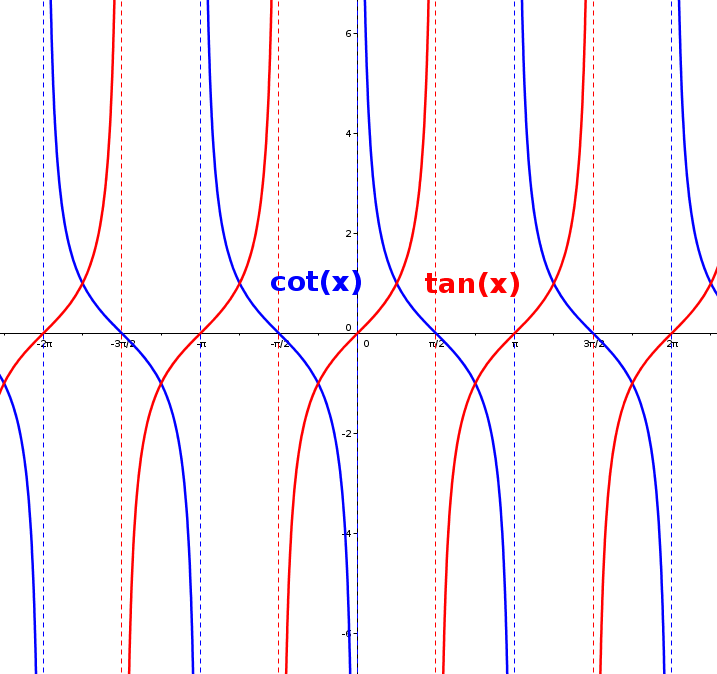
Analitzem-ho amb detall utilitzant els límits. Analitzem per exemple $f (x) = \cot x$ en $x = 0$ que és un punt de tall de la tangent amb l'eix OX:

$f (0) = \cot 0 = \frac{1}{\tan 0} = \frac{1}{0} = ∄$

$\lim_{x \to 0} f (x) = \lim_{x \to 0} \cot x = \lim_{x \to 0} \frac{1}{\tan x} = \frac{1}{\tan 0} = \frac{1}{0} = ∞$
I, per tant, caldria fer límits laterals per tenir més informació de l'asímptota.
- per l'esquera: $\lim_{x \to 0^{-}} f (x) = \lim_{x \to 0^{-}} \cot x = \lim_{x \to 0^{-}} \frac{1}{\tan x} = \frac{1}{\tan 0^{-}} = \frac{1}{0^{-}} = - ∞$
- per la dreta: $\lim_{x \to 0^{+}} f (x) = \lim_{x \to 0^{+}} \cot x = \lim_{x \to 0^{+}} \frac{1}{\tan x} = \frac{1}{\tan 0^{+}} = \frac{1}{0^{+}} = + ∞$

El mateix ens passaria en qualsevol dels punts on s'anul·la la funció $f (x) = \tan x$ , que recordem que són $x = k π \forall k \in ℤ$

Podeu analitzar vosaltres el que li passaria a la funció $f (x) = \tan x$ en els punts on s'anul·la la funció $f (x) = \cot x$ . Per exemple $f (x) = \tan x$ en $x = \frac{π}{2}$ que és un punt de tall de la cotangent amb l'eix OX:

Secant

Recorda que

\sec α = \frac{1}{\cos α}

Anomenem funció secant a la funció que a cada nombre real $x$ li fa correspondre el valor de la secant de l'angle que mesura $x$ radians, i l'expressem així:

f (x) = \sec x

També volem saber com és el seu gràfic i les seves principals característiques.

f (x) = \sec (x)

Domini: $ℝ \sim {\frac{π}{2} + k π}, \forall k \in ℤ$
Recorregut: $(- ∞, - 1] \cup [1, + ∞)$
Té infinites discontinuïtats asimptòtiques
Funció periòdica de període $2 π$
És simètrica respecte l'eix OY
Punts importants

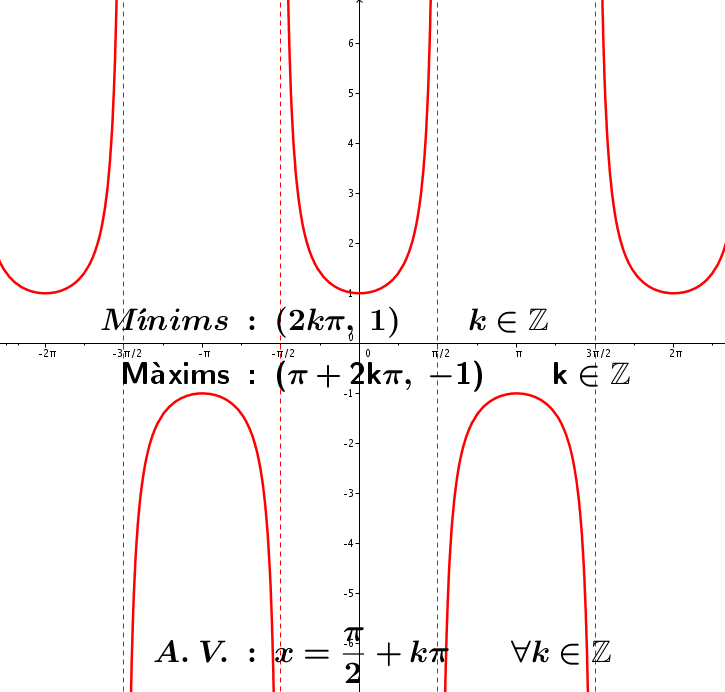
És important que miris conjuntament els gràfics de les funcions $\sec x$ i $\cos x$ . Observa que en els punts de tall amb l'eix OX de $\cos x$ és on hi té les asímptotes verticals la $\sec x$ . I en els punts on $\cos x = 1$ també és $\sec x = 1$

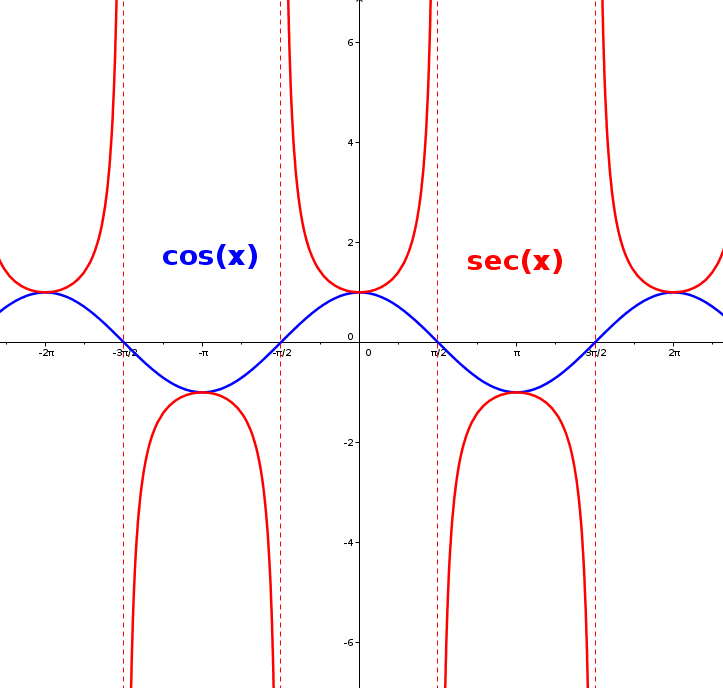
Analitzem-ho amb detall utilitzant els límits. Analitzem per exemple $f (x) = \sec x$ en $x = \frac{π}{2}$ que és un punt de tall del cosinus amb l'eix OX:

$f (\frac{π}{2}) = \sec \frac{π}{2} = \frac{1}{\cos \frac{π}{2}} = \frac{1}{0} = ∄$

$\lim_{x \to \frac{π}{2}} f (x) = \lim_{x \to \frac{π}{2}} \sec x = \lim_{x \to \frac{π}{2}} \frac{1}{\cos x} = \frac{1}{\cos \frac{π}{2}} = \frac{1}{0} = ∞$
I, per tant, caldria fer límits laterals per tenir més informació de l'asímptota.
- per l'esquera: $\lim_{x \to {\frac{π}{2}}^{-}} f (x) = \lim_{x \to {\frac{π}{2}}^{-}} \sec x = \lim_{x \to {\frac{π}{2}}^{-}} \frac{1}{\cos x} = \frac{1}{\cos {\frac{π}{2}}^{-}} = \frac{1}{0^{+}} = + ∞$
- per la dreta: $\lim_{x \to {\frac{π}{2}}^{+}} f (x) = \lim_{x \to {\frac{π}{2}}^{+}} \sec x = \lim_{x \to {\frac{π}{2}}^{+}} \frac{1}{\cos x} = \frac{1}{\cos {\frac{π}{2}}^{+}} = \frac{1}{0^{-}} = - ∞$

El mateix ens passaria en qualsevol dels punts on s'anul·la la funció $f (x) = \cos x$ .

Analitzem ara que val $f (x) = \sec x$ en els punts on el cosinus val $1$ . Per exemple, en $x = 0$ .

$f (0) = \sec 0 = \frac{1}{\cos 0} = \frac{1}{1} = 1$

És a dir,

\cos (0)

és

1

\sec (0)

també és

1

. Això és el que passa en tots els

2 k π \forall k \in ℤ

Anàlogament on

\cos x

és

- 1

\sec x

també és

- 1

. Pots analitzar el cas

x = π

Cosecant

Recorda que

\csc α = \frac{1}{\sin α}

Anomenem funció cosecant a la funció que a cada nombre real

x

li fa correspondre el valor de la cosecant de l'angle que mesura

x

radians, i l'expressem així:

f (x) = \csc x

També volem saber com és el seu gràfic i les seves principals característiques.

f (x) = \csc (x)

Domini: $ℝ \sim {k π}, \forall k \in ℤ$
Recorregut: $(- ∞, - 1] \cup [1, + ∞)$
Té infinites discontinuïtats asimptòtiques
Funció periòdica de període $2 π$
És simètrica respecte l'origen
Punts importants

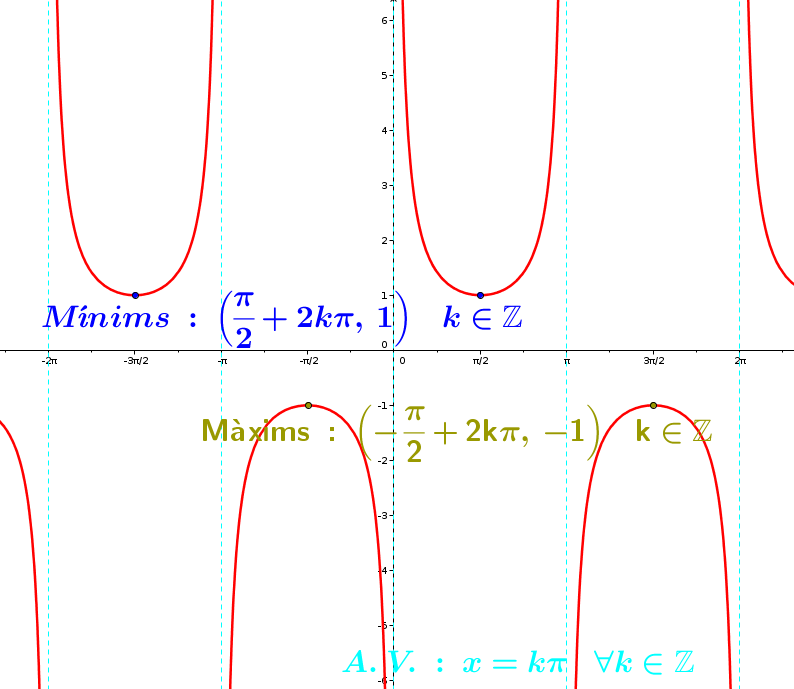
És important que miris conjuntament els gràfics de les funcions $\csc x$ i $\sin x$ . Observa que en els punts de tall amb l'eix OX de $\sin x$ és on hi té les asímptotes verticals la $\csc x$ . I en els punts on $\sin x = - 1$ també és $\csc x = - 1$

Analitzem-ho amb detall utilitzant els límits. Analitzem per exemple $f (x) = \csc x$ en $x = π$ que és un punt de tall del sinus amb l'eix OX:

$f (π) = \csc π = \frac{1}{\sin π} = \frac{1}{0} = ∄$

$\lim_{x \to π} f (x) = \lim_{x \to π} \csc x = \lim_{x \to π} \frac{1}{\sin x} = \frac{1}{\sin π} = \frac{1}{0} = ∞$
I, per tant, caldria fer límits laterals per tenir més informació de l'asímptota.
- per l'esquera: $\lim_{x \to π^{-}} f (x) = \lim_{x \to π^{-}} \csc x = \lim_{x \to π^{-}} \frac{1}{\sin x} = \frac{1}{\sin π^{-}} = \frac{1}{0^{+}} = + ∞$
- per l'esquera: $\lim_{x \to π^{+}} f (x) = \lim_{x \to π^{+}} \csc x = \lim_{x \to π^{+}} \frac{1}{\sin x} = \frac{1}{\sin π^{+}} = \frac{1}{0^{-}} = - ∞$

El mateix ens passaria en qualsevol dels punts on s'anul·la la funció $f (x) = \sin x$ .

Analitzem ara que val $f (x) = \csc x$ en els punts on el sinus val $- 1$ . Per exemple, en $x = - \frac{π}{2}$ .

$f (- \frac{π}{2}) = \csc (- \frac{π}{2}) = \frac{1}{\sin (- \frac{π}{2})} = \frac{1}{- 1} = - 1$

És a dir,

\sin (- \frac{π}{2})

és

- 1

\csc (- \frac{π}{2})

també és

- 1

. Això és el que passa en tots els

x = - \frac{π}{2} + 2 k π \forall k \in ℤ

Anàlogament on

\sin x

és

1

\csc x

també és

1

. Pots analitzar el cas

x = \frac{π}{2}

Identitats i equacions trigonomètriques

De les igualtats matemàtiques on apareixen funcions trigonomètriques en diem igualtats trigonomètriques.

Ja saps que tenim dos tipus d'igualtats, les que són certes sempre, posem el que posem al lloc de les variables, i diem que són identitats i les que no són sempre certes, que anomenem equacions, poden ser certes per algun/s valor/s que posem al lloc de les variables, que ara anomenem incògnites.

Per exemple, la igualtat

\sin^{2} x + \cos^{2} x = 1

saps que és certa sempre, independentment del valor que posem al lloc de la

x

. És la relació fonamental de la trigonometria. És una identitat trigonomètrica. En canvi,

\sin x = \frac{1}{2}

no és sempre certa. És certa si la

x

la substituïm per

\frac{π}{6}

, o per

\frac{5 π}{6}

. És, per tant, una equació trigonomètrica, i els valors

x = \frac{π}{6}

x = \frac{5 π}{6}

són solucions de l'equació. Però aquesta equació en té moltes més de solucions, més endavant mirarem d'escriure-les totes.

Hi ha equacions que no tenen solució, per exemple:

\sin x = 2

. Això vol dir que no hi ha cap valor que puguem posar al lloc de la

x

que faci certa la igualtat.

Les identitats les hem de demostrar, comprovar o verificar. Les equacions les hem de resoldre.

Ja coneixes moltes identitats trigonomètriques, per exemple les identitats Pitagòriques:

\sin^{2} x + \cos^{2} x = 1

\tan^{2} x + 1 = \sec^{2} x

1 + \cot^{2} x = \csc^{2} x

Les relacions entre les raons trigonomètriques:

\tan x = \frac{\sin x}{\cos x}

\cot x = \frac{\cos x}{\sin x}

\sec x = \frac{1}{\cos x}

\csc x = \frac{1}{\sin x}

\cot x = \frac{1}{\tan x}

Podríem continuar amb totes les fórmules que relacionen raons trigonomètriques d'angles complementaris, suplementaris, ..., les raons trigonomètriques de la suma d'angles, de la resta, de l'angle doble, ...

Podem utilitzar les identitats per simplificar expressions trigonomètriques. A vegades és possible reescriure una expressió trigonomètrica que sembla complicada d'una altra manera molt més simple. És com si nosaltres haguèssim de trobar una identitat trigonomètrica.

Simplificar expressions trigonomètriques
Demostrar identitats trigonomètriques
Resoldre equacions trigonomètriques

Demostrar identitats trigonomètriques

És fàcil decidir que una igualtat no és una identitat. N'hi ha prou en trobar algun valor que posat al lloc de la variable faci falsa la igualtat.

Per exemple, la igualtat:

\sin x + \cos x = 1

no és una identitat, perquè quan

x = \frac{π}{4}

, tenim que:

\sin \frac{π}{4} + \cos \frac{π}{4} = 1

és fals. Vegem-ho:

\sin \frac{π}{4} + \cos \frac{π}{4} = \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} = \frac{2 \sqrt{2}}{2} = \sqrt{2} \neq 1

Recordem que una identitat ha de ser certa per a qualssevol valors que posem al lloc de la variable. Per tant, si en trobem un pel qual no és certa, ja podem afirmar que no és una identitat.

Per a demostrar que una igualtat és una identitat, hem de transformar un membre de la igualtat en l'altre en una sèrie d'etapes, cadascuna de les quals ha de ser una identitat.

RECOMANACIONS

Començar amb un membre. L'objectiu és transformar-lo en l'altre. Normalment és més fàcil començar amb el membre més complicat.
Utilitzar identitats conegudes. Utilitzar l'àlgebra i les identitats que ja coneixes per anar canviant el membre amb el que has començat. Si hi ha fraccions pot ser hauràs de fer les operacions, factoritzar, simplificar, ...
Convertir a sinus i cosinus. Si quedes encallat i no saps què fer, pot ajudar-te canviar totes les funcions trigonomètriques pel seu equivalent en sinus i cosinus.

EXEMPLE 1

Demostra algebraicament la següent identitat:

\cos t (\sec t - \cos t) = \sin^{2} t

Solució

A l'exemple anterior hem fet la demostració algebraica, que és la millor. També ens pot ajudar fer una Comprovació gràfica o una Comprovació numèrica . Però com hem dit, la manera correcta de demostrar identitats és la demostració algebraica.

Tornem, doncs, amb més exemples de demostracions algebraiques.

Exemple 2
Exemple 3
Exemple 4

Comprovació gràfica

Aquesta comprovació gràfica consisteix en representar gràficament, amb algun programa d'ordinador, calculadora, ..., els dos membres de la igualtat. Si els gràfics no coincideixen, no és una identitat. Aquesta comprovació gràfica no té el valor de la demostració algebraica perquè podria ser que coincidissin en la part que veiem a la pantalla però no coincidissin en alguna part que en queda fora. I, també, perquè els gràfics, a vegades, ens enganyen.

A continuació pots veure que la igualtat:

\sin^{2} x - \cos^{2} x = {(\sin x - \cos x)}^{2}

no és una identitat. (Només ens cal posar al lloc adequat cada membre de la igualtat)

De fet, aquí també podríes comprovar si has fet bé una simplificació d'una expressió trigonomètrica. Pots practicar-ho amb la simplificació que s'ha vist a l'Exemple 1 de l'apartat anterior.

\cos x + \tan x \sin x = \sec x

Comprovació numèrica

Amb la comprovació numèrica, aquí pots veure una identitat que abans hem obtingut en una simplificació.

Aquesta comprovació numèrica té els mateixos perills que la gràfica, podria passar que coincidissin en els valors que posem però no en d'altres. És per això que la manera correcta de demostrar identitats és la demostració algebraica.

Exemple 2

EXEMPLE 2

Demostra la identitat:

2 \tan α \sec α = \frac{1}{1 - \sin α} - \frac{1}{1 + \sin α}

Solució

Exemple 3

EXEMPLE 3

Demostra la identitat:

\frac{\cos u}{1 - \sin u} = \sec u + \tan u

Solució

Exemple 4

EXEMPLE 4

Demostra la identitat:

\frac{1 + \cos α}{\cos α} = \frac{\tan^{2} α}{\sec α - 1}

Solució

Resoldre equacions trigonomètriques

Ja hem dit que les equacions trigonomètriques són igualtats trigonomètriques que a diferència de les identitats trigonomètriques no són certes per a tots els valors que posem al lloc de la variable.

A les equacions, les variables, les anomenem incògnites.

Ja hem posat l'exemple de

\sin x = \frac{1}{2}

. És certa si la

x

la substituïm per

\frac{π}{6}

, o per

\frac{5 π}{6}

. És una equació trigonomètrica, i els valors

x = \frac{π}{6}

x = \frac{5 π}{6}

són solucions de l'equació. Però aquesta equació en té moltes més de solucions, ara mirarem d'escriure-les totes. Aquí, donarem sempre les solucions en radians.

Hi ha equacions que no tenen solució, per exemple:

\sin x = 2

. Això vol dir que no hi ha cap valor que puguem posar al lloc de la

x

que faci certa la igualtat.

Les equacions trigonomètriques acabaran reduïdes a uns tipus bàsics, que són els que veurem en aquests primers exemples. Aquests els podrem fer sense calculadora i trobarem solucions exactes, has de recordar el valor exacte de les raons trigonomètriques dels angles importants de cada quadrant. Pots consultar aquesta Ajuda .

Exemple 1 $\sin θ = \frac{1}{2}$
Exemple 2 $\cos θ = - \frac{\sqrt{2}}{2}$
Exemple 3 $\tan θ = \sqrt{3}$

Anem a veure ara equacions també bàsiques però en les que necessitarem calculadora i donarem solucions aproximades.

Exemple 4 $\cos x = m$
Exemple 5 $\tan x = m$
Exemple 6 $\sin x = m$

En cas que l'equació trigonomètrica sigui més complexa, la resolució requereix, en general, la transformació en una altra equació equivalent més senzilla, semblant a una dels tipus bàsics.

Exemple 7 $\cos x = \cot x$
Exemple 8 $2 \cos^{2} x = 7 \cos x - 3$
Exemple 9 $5 \cos x \sin x = - 2 \sin x$

També ens podem trobar equacions trigonomètriques on les funcions trigonometriques actuen sobre múltiples d'un angle, per exemple $2 x, 3 x, \frac{x}{2},$ ... Resoldrem l'equació per aquest múltiple d'angle i finalment trobarem l'angle $x$ dividint o multiplicant.

Exemple 10 $2 \sin 3 θ - 1 = 0$
Exemple 11 $\sqrt{3} \tan \frac{θ}{2} - 1 = 0$

Altres vegades cal utilitzar identitats trigonomètriques o elevar al quadrat els dos membres per poder resoldre l'equació. En aquest darrer cas, recordeu que s'han de comprovar les solucions.

Exemple 12 $1 + \sin θ = 2 \cos^{2} θ$
Exemple 13 $\sin 2 θ - \cos θ = 0$
Exemple 14 $\cos θ + 1 = \sin θ$

Ajuda

Circumferència trigonomètrica

raons trigonomètriques

Exemple 1

EXEMPLE 1

Resol l'equació:

\sin θ = \frac{1}{2}

Solució

Exemple 2

EXEMPLE 2

Resol l'equació:

\cos θ = - \frac{\sqrt{2}}{2}

i dóna vuit solucions concretes.

Solució

Exemple 3

EXEMPLE 3

Resol l'equació:

\tan θ = \sqrt{3}

i dóna vuit solucions concretes.

Solució

Exemple 4

EXEMPLE 4

Resol l'equació:

\cos x = 0.25

i dóna quatre solucions concretes aproximades.

Solució

Exemple 5

EXEMPLE 5

Resol l'equació:

\tan x = - 0.96

i dóna quatre solucions concretes aproximades.

Solució

Exemple 6

EXEMPLE 6

Resol l'equació:

\sin x = - 0.42

i dóna quatre solucions concretes aproximades.

Solució

Exemple 7

EXEMPLE 7

Resol l'equació:

\cos x = \cot x

Solució

Exemple 8

EXEMPLE 8

Resol l'equació:

2 \cos^{2} x = 7 \cos x - 3

Solució

Exemple 9

EXEMPLE 9

Resol l'equació:

5 \cos x \sin x = - 2 \sin x

Solució

Exemple 10

EXEMPLE 10

Resol l'equació:

2 \sin 3 θ - 1 = 0

Solució

Exemple 11

EXEMPLE 11

Resol l'equació:

\sqrt{3} \tan \frac{θ}{2} - 1 = 0

Solució

Exemple 12

EXEMPLE 12

Resol l'equació:

1 + \sin θ = 2 \cos^{2} θ

Solució

Exemple 13

EXEMPLE 13

Resol l'equació:

\sin 2 θ - \cos θ = 0

Solució

Exemple 14

EXEMPLE 14

A l'interval $[0, 2 π)$ , resol l'equació:

\cos θ + 1 = \sin θ

Solució

Simplificar expressions trigonomètriques

Ja hem dit que simplificar una expressió trigonomètrica és reescriure l'expressió trigonomètrica que sembla complicada d'una altra manera molt més simple.

EXEMPLE 1

Simplifica l'expressió:

\cos x + \tan x \sin x

Solució

EXEMPLE 2

Simplifica l'expressió:

\frac{\sin θ}{\cos θ} + \frac{\cos θ}{1 + \sin θ}

Solució

Funció sinus
- Característiques de la funció sinus
- Transformacions de la funció sinus
Funció cosinus
- Característiques de la funció cosinus
- Transformacions de la funció cosinus
Funció tangent
- Característiques de la funció tangent
Funcions inverses de les funcions trigonomètriques
- Repassar el concepte de Funció inversa
- La funció arc sinus
- La funció arc cosinus
- La funció arc tangent
Altres funcions trigonomètriques
Identitats i equacions trigonomètriques

funcions, identitats i equacions trigonomètriques.
: , interactive mathematics, interactive math, server side interactivity

The most recent version