Trigonometria a 1r de BAT

Provinent de la llengua grega, la paraula trigonometria significa "mesura de triangles". Inicialment, la trigonometria tractava les relacions entre els costats i els angles dels triangles i es va utilitzar en el desenvolupament de l'astronomia, la navegació i la topografia. Amb el desenvolupament del càlcul i les ciències físiques al segle XVII, va sorgir una perspectiva diferent que veu les raons trigonomètriques clàssiques com funcions amb el conjunt dels nombres reals com els seus dominis. En conseqüència, les aplicacions de la trigonometria s'han ampliat per incloure a un gran nombre de fenòmens físics que impliquen rotacions i vibracions. Entre aquests fenòmens s'inclouen les ones de so, els raigs de llum, òrbites planetàries, cordes vibrants, pèndols, i les òrbites de les partícules atòmiques.

Pots començar amb aquesta Introducció històrica .

Preparat? Vinga, doncs: Trigonometria !!!!!!!!!!!!!!!

Measurement of the Earth's circumference

On the Sizes and Distances (Aristarchus)

El metro, el meridiano de París y Barcelona

Ingeniería Romana. Cap.1 Acueductos . Especialment els 13 minuts inicials.

1. Angles
2. Mesurar angles en graus
3. Mesurar angles en radians
4. Equivalència entre graus i radians
5. Mesura principal d'un angle
6. Raons trigonomètriques d'un angle agut
7. Resolució de triangles rectangles
8. Raons trigonomètriques d'un angle qualsevol
9. Línies trigonomètriques
10. Reducció al primer quadrant
    • Angle del 2n quadrant
    • Angle del 3r quadrant
    • Angle del 4t quadrant
11. Relació entre les raons trigonomètriques d'angles oposats
12. Relació entre les raons trigonomètriques d'angles complementaris
13. Raons trigonomètriques dels angles importants
14. Relacions entre les raons trigonomètriques d'un mateix angle
15. Fórmules d'addició
    • Raons trigonomètriques d'una suma d'angles
    • Raons trigonomètriques d'una resta d'angles
    • Raons trigonomètriques de l'angle doble
    • Raons trigonomètriques de l'angle meitat
16. Resolució de triangles obliquangles
    • Coneguts els tres costats
    • Coneguts dos costats i l'angle que formen
    • Coneguts un costat i dos o tres angles
    • Coneguts dos costats i l'angle oposat a un d'ells

Una unitat per mesurar angles és el grau, denotat amb el símbol ${}^{\circ }$. L'angle que fa una volta sencera mesura 360 ${}^{\circ }$. Un angle de 1 ${}^{\circ }$ és ${\displaystyle \frac{1}{360}}$ part d'una volta sencera (o angle complet).

Pots veure a continuació alguns angles en posició estàndard mesurats en graus:

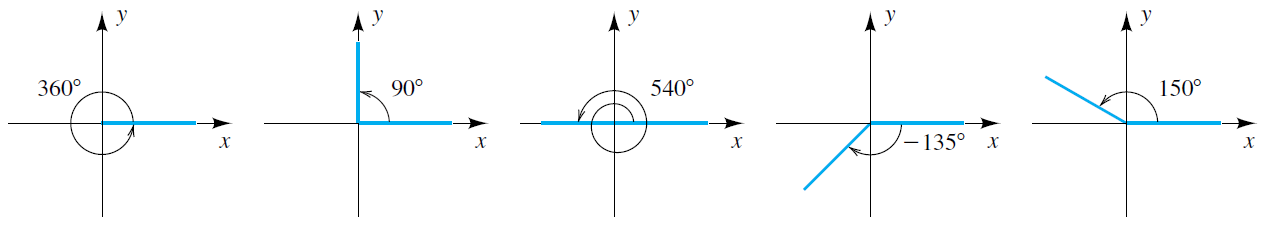
Pots modificar el valor de l'angle i veure'l en posició estàndard.

Exercicis:

• Has d'encertar l'angle dibuixat 1
• Has d'encertar l'angle dibuixat 2

A més dels graus sexagesimals que ja coneixes, hi ha una altra unitat per mesurar els angles. És el radian o radiant (rad).

Si fem coincidir el vèrtex d'un angle amb el centre d'una circumferència, l'angle determina en la circumferència un arc.

DEFINICIÓ Un angle d'un radian és un angle $\theta$ que intercepta en una circumferència un arc $s$ que té la mateixa longitud que el radi $r$ amb el que s'ha traçat.
	$\mathrm{arc}=\mathrm{radi}\to \theta =1$ rad

La longitud $l$ d'una circumferència és $l=2\pi r$. És a dir, l'arc corresponent a un angle complet fa $s=2\pi r$ , això és, $2\pi$ vegades el radi. Per tant, l'angle complet té una mesura de $2\pi$ rad. Com que $2\pi \approx 6.28$, una circumferència sencera conté més de 6 vegades la longitud del radi.

D'aquesta manera, la relació que hi ha entre un angle $\theta$ en radians i la longitud $s$ de l'arc associat ve donada per: $s=\theta \cdot r$

És a dir, la longitud d'un arc de circumferència és igual a l'angle mesurat en radians multiplicat per la longitud del radi.

Aquí pots veure la mesura en radians d'alguns dels angles més habituals.

Sempre que es pugui, el angles en radians els expressarem com a múltiples o fraccions de $\pi$. Per exemple: $5\pi ,{\displaystyle \frac{3\pi }{2}},{\displaystyle \frac{\pi }{9}}$.

Ves modificant els valors del radi i de la longitud de l'arc i observa com va canviant el valor de l'angle.

Exercicis:

• Angle i arc
• Angle en graus d'un arc
• El radian
• Angle en radians d'un arc

Ja saps que un angle complet mesura ${360}^{\circ }$ o $2\pi$ rad. Així, ja tens l'equivalència:

${360}^{\circ }=2\pi$ rad.
Qualsevol fracció o múltiple d'aquesta equivalència també ho serà. Per tant:

${180}^{\circ }=\pi$ rad	fent la meitat de l'anterior
${60}^{\circ }={\displaystyle \frac{\pi }{3}}$ rad	fent un terç de l'anterior
${120}^{\circ }={\displaystyle \frac{2\pi }{3}}$ rad	fent el doble de l'anterior

Altres vegades caldrà donar valors aproximats: ${41}^{\circ }=0.7156$ rad, ${128}^{\circ }=2.2340$ rad.

En general, per passar de graus a radians pots multiplicar per ${\displaystyle \frac{\pi \mathrm{rad}}{{180}^{\circ }}}$ i per fer-ho de radians a graus per ${\displaystyle \frac{{180}^{\circ }}{\pi \mathrm{rad}}}$.

Exercicis:

• Passar de graus sexagesimals a radians 1
• Passar de graus sexagesimals a radians 2
• Passar de radians a graus sexagesimals 1
• Passar de radians a graus sexagesimals 2

Trobar la mesura principal d'un angle

Mirant els angles com a girs també té sentit parlar d'angles de més de ${360}^{\circ }$. Un angle de ${400}^{\circ }$ entenem que vol dir que s'ha girat una volta sencera i ${40}^{\circ }$ de la volta següent.

L'angle de ${390}^{\circ }$ queda en la mateixa posició que el de ${30}^{\circ }$, el de $-{150}^{\circ }$ que el de ${210}^{\circ }$ i el de $-{380}^{\circ }$ que el de ${340}^{\circ }$. Fer aquestes equivalències és el que en diem reduir un angle al primer gir o trobar la mesura principal de l'angle. És a dir, donat un angle es tracta de trobar-ne un altre de positiu i menor de ${360}^{\circ }$ que tingui el mateix costat final.

Cal fer una divisió entera per ${360}^{\circ }$ per conèixer el quocient enter (seran les voltes senceres) i el residu (l'angle reduït al primer gir). Si l'angle és negatiu has de fer alguna cosa més.

Exercici:

• Trobar la mesura principal d'un angle

Exercicis:

• Raons trigonomètriques d'un angle agut
• Raons trigonomètriques de l'angle de \(45^\circ)
• Raons trigonomètriques dels angles de \(30^\circ) i \(60^\circ)

Les eines que disposem per resoldre qualsevol triangle rectangle són les següents:

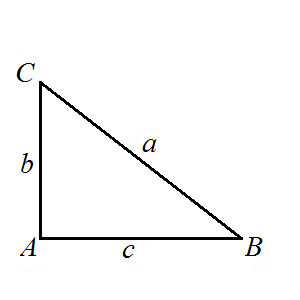
Teorema de Pitàgores: $a^2=b^2+c^2$ Els angles aguts sumen ${90}^{\circ }$ : $B+C={90}^{\circ }$ Les raons trigonomètriques dels angles aguts: $\sin B={\displaystyle \frac{b}{a}};\cos B={\displaystyle \frac{c}{a}};\tan B={\displaystyle \frac{b}{c}}$ $\sin C={\displaystyle \frac{c}{a}};\cos C={\displaystyle \frac{b}{a}};\tan C={\displaystyle \frac{c}{b}}$

Exercicis:

• Resolució de triangles rectangles 1
• Resolució de triangles rectangles 2
• Resolució de triangles rectangles 3
• Resolució de triangles rectangles 4
• Triangle isòsceles
• Angle d'elevació
• Altura d'un arbre
• Helicòpter
• Disseny d'un robot 1
• Disseny d'un robot 2

Altres raons trigonomètriques

Les anteriors són les raons trigonomètriques més importants, però n'hi ha d'altres que també cal conèixer, són la cotangent, la secant i la cosecant.

Es defineixen així:

$\cot (x)={\displaystyle \frac{1}{\tan (x)}}$

$\sec (x)={\displaystyle \frac{1}{\cos (x)}}$

$\mathrm{cosec}(x)=\csc (x)={\displaystyle \frac{1}{\sin (x)}}$

Fixa't que la cosecant es pot expressar de dues formes diferents: $\mathrm{cosec}(x)$ o $\csc (x)$.
Exercici:

• Sinus i cosinus d'un angle qualsevol

Cal veure que cada raó trigonomètrica té associat un segment. Aquests segments els anomenem línies trigonomètriques.

Altra versió

Exercicis:

• Línies trigonomètriques
• Línies trigonomètriques 1
• Línies trigonomètriques 2
• Raons trigonomètriques d'un angle qualsevol
• Raons trigonomètriques d'un angle qualsevol

Les raons trigonomètriques de qualsevol angle es poden relacionar amb les d'un altre angle situat al 1r quadrant. La manera de fer-ho depèn del quadrant al que pertanyi l'angle.

• Angle del 2n quadrant
• Angle del 3r quadrant
• Angle del 4t quadrant

Si $\alpha$ és un angle del 3r quadrant, les seves raons trigonomètriques es poden relacionar amb les d'un altre angle situat al 1r quadrant. Mira de entendre-ho a la següent figura. Pots modificar el valor de l'angle.

Els angles $\alpha$ i $\alpha -{180}^{\circ }$ difereixen en ${180}^{\circ }$. Per això les relacions anteriors també es coneixen com Relacions entre les raons trigonomètriques de dos angles que difereixen en ${180}^{\circ }$.

Si $\alpha$ és un angle del 2n quadrant, les seves raons trigonomètriques es poden relacionar amb les d'un altre angle situat al 1r quadrant. Mira de entendre-ho a la següent figura. Pots modificar el valor de l'angle.

Els angles $\alpha$ i ${180}^{\circ }-\alpha$ són suplementaris donat que la seva suma és de ${180}^{\circ }$. Per això les relacions anteriors també es coneixen com Relacions entre les raons trigonomètriques de dos angles suplementaris.

Si $\alpha$ és un angle del 4t quadrant, les seves raons trigonomètriques es poden relacionar amb les d'un altre angle situat al 1r quadrant. Mira de entendre-ho a la següent figura. Pots modificar el valor de l'angle.

Recorda que dos angles són oposats si la seva suma és $0^{\circ }$. Així, si un d'ells és $\alpha$, l'altre serà $-\alpha$.

Exercici:

• Relació entre les raons trigonomètriques de diferents angles

Recorda que dos angles són complementaris si la seva suma és ${90}^{\circ }$. Així, si un d'ells és $\alpha$, l'altre serà ${90}^{\circ }-\alpha$.

Exercici:

• Relació entre les raons trigonomètriques d'angles complementaris

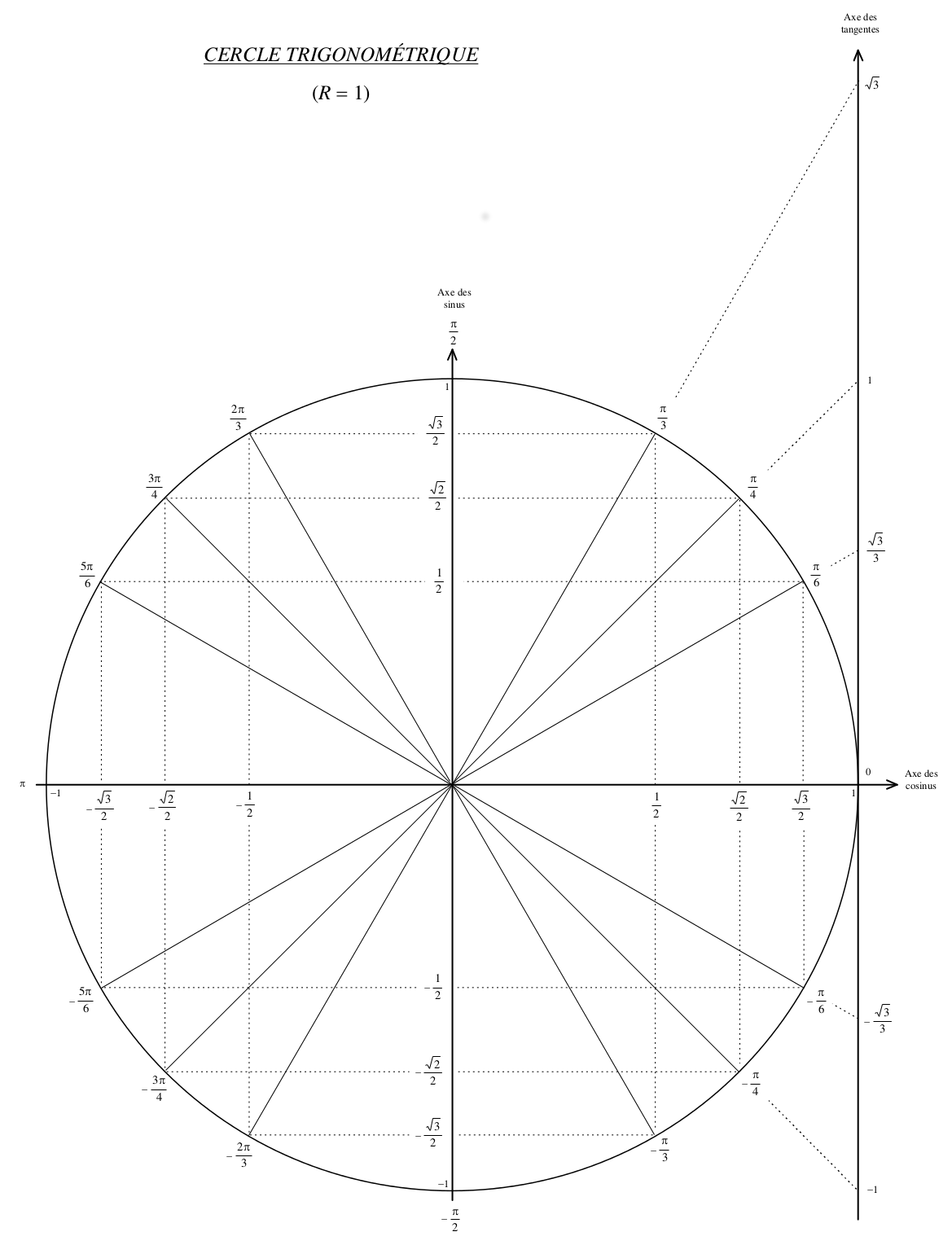
Atès que a la circumferència unitat $\sin \alpha =y$ , $\cos \alpha =x$ i $\tan \alpha ={\displaystyle \frac{y}{x}}$, ja tenim la primera relació entre les raons trigonomètriques d'un mateix angle:

$\tan \alpha ={\displaystyle \frac{\sin \alpha }{\cos \alpha }}$

Hi ha altres relacions anomenades Relacions Pitagòriques. Aplicant el Teorema de Pitàgores a cadascun dels triangles rectangle següents, tenim:

	$(\sin \alpha {)}^2+(\cos \alpha {)}^2=1^2$ Relació fonamental de la Trigonometria ${\sin }^2\alpha +{\cos }^2\alpha =1$
	$1^2+(\tan \alpha {)}^2=(\sec \alpha {)}^2$ $1+{\tan }^2\alpha ={\sec }^2\alpha$
	$1^2+(\cot \alpha {)}^2=(\mathrm{cosec}\alpha {)}^2$ $1+{\cot }^2\alpha ={\mathrm{cosec}}^2\alpha$

Al contrari del que es podria pensar:

$\cos (\alpha +\beta )\ne \cos \alpha +\cos \beta$

No ens hauria de sorprendre per què ja tenim experiència en altres situacions semblants. Recorda que:

$\sqrt{64+36}=\sqrt{100}=10$

Mentre que

$\sqrt{64}+\sqrt{36}=8+6=14$

Així, doncs

$\sqrt{64+36}\ne \sqrt{64}+\sqrt{36}$

I, en general

$\sqrt{a+b}\ne \sqrt{a}+\sqrt{b}$

Amb les raons trigonomètriques ens passa una cosa semblant. Fixa't:

$\sin (30+60)=\sin (90)=1$

Mentre que

$\sin (30)+\sin (60)={\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sqrt{3}}{2}}={\displaystyle \frac{1+\sqrt{3}}{2}}\approx 1.3660$

Així, doncs

$\sin (30+60)\ne \sin (30)+\sin (60)$

I, en general

$\sin (\alpha +\beta )\ne \sin \alpha +\sin \beta$

Hem d'intentar trobar, doncs, unes expressions que ens permetin desenvolupar les raons trigonomètriques d'una suma, d'una resta, de l'angle doble i de l'angle meitat.

Es demostraran en els següents apartats i aquí les posem en forma de resum:

Exercicis:

• Raons trigonomètriques de l'angle suma
• Raons trigonomètriques de l'angle resta
• Raons trigonomètriques de l'angle doble
• Raons trigonomètriques de l'angle meitat

Volem trobar una expressió que ens permeti desenvolupar el cosinus d'una suma d'angles, és a dir, donats dos angles $\alpha$ i $\beta$ , volem trobar $\cos (\alpha +\beta )$. Ens ajudarem de la figura següent:

Pots veure a la figura que s'ha representat l'angle $\alpha +\beta$ a la circumferència goniomètrica i uns quants segments. Observa que:

$\cos (\alpha +\beta )=\mathrm{OK}$

i que:

$\mathrm{OK}=\mathrm{OL}-\mathrm{KL}$

Així que, de moment:

$\cos (\alpha +\beta )=\mathrm{OK}=\mathrm{OL}-\mathrm{KL}$

És important que entenguis que els dos angles pintats de color verd són iguals.

Treballant amb el triangle rectangle $\mathrm{OLI}$ tenim:

$\cos \alpha ={\displaystyle \frac{\mathrm{OL}}{\mathrm{OI}}}⟶\mathrm{OL}=\cos \alpha \cdot \mathrm{OI}$

Treballant amb el triangle rectangle $\mathrm{OIG}$ tenim:

$\cos \beta ={\displaystyle \frac{\mathrm{OI}}{1}}⟶\mathrm{OI}=\cos \beta$

Per tant:

$\mathrm{OL}=\cos \alpha \cdot \mathrm{OI}=\cos \alpha \cdot \cos \beta$

Per altra banda, $\mathrm{KL}=\mathrm{MI}$, i treballant amb el triangle rectangle $\mathrm{MIG}$, tenim:

$\sin \alpha ={\displaystyle \frac{\mathrm{MI}}{\mathrm{GI}}}⟶\mathrm{MI}=\sin \alpha \cdot \mathrm{GI}$

Treballant amb el triangle rectangle $\mathrm{OIG}$ tenim:

$\sin \beta ={\displaystyle \frac{\mathrm{GI}}{1}}⟶\mathrm{GI}=\sin \beta$

Per tant:

$\mathrm{KL}=\mathrm{MI}=\sin \alpha \cdot \mathrm{GI}=\sin \alpha \cdot \sin \beta$

I, tornant a l'expressió inicial, tenim

$\cos (\alpha +\beta )=\mathrm{OK}=\mathrm{OL}-\mathrm{KL}=\cos \alpha \cdot \cos \beta -\sin \alpha \cdot \sin \beta$

Ja tenim, doncs, la fórmula del cosinus d'una suma d'angles:

Per trobar la fórmula del sinus d'una suma d'angles també podríem raonar a partir de la figura anterior, però serà més curt si ho fem d'una altra manera. Fixa't:

$\sin (\alpha +\beta )=\cos [90-(\alpha +\beta )]=\cos [(90-\alpha )+(-\beta )]=$

I utilitzant la fórmula anterior del cosinus d'una suma d'angles, continua:

$=\cos (90-\alpha )\cdot \cos (-\beta )-\sin (90-\alpha )\cdot \sin (-\beta )=$

I utilitzant relacions ja conegudes continua:

$=\sin \alpha \cdot \cos \beta -\cos \alpha \cdot (-\sin \beta )=\sin \alpha \cdot \cos \beta +\cos \alpha \cdot \sin \beta$

Tenim, doncs, la fórmula del sinus d'una suma d'angles:

Anem a trobar, ara, la fórmula de la tangent:

$\tan (\alpha +\beta )={\displaystyle \frac{\sin (\alpha +\beta )}{\cos (\alpha +\beta )}}={\displaystyle \frac{\sin \alpha \cdot \cos \beta +\cos \alpha \cdot \sin \beta }{\cos \alpha \cdot \cos \beta -\sin \alpha \cdot \sin \beta }}=$

Dividim numerador i denominador d'aquesta fracció per $\cos \alpha \cdot \cos \beta$ i simplifiquem:

$={\displaystyle \frac{{\displaystyle \frac{\sin \alpha \cdot \cos \beta }{\cos \alpha \cdot \cos \beta }}+{\displaystyle \frac{\cos \alpha \cdot \sin \beta }{\cos \alpha \cdot \cos \beta }}}{{\displaystyle \frac{\cos \alpha \cdot \cos \beta }{\cos \alpha \cdot \cos \beta }}-{\displaystyle \frac{\sin \alpha \cdot \sin \beta }{\cos \alpha \cdot \cos \beta }}}}={\displaystyle \frac{\tan \alpha +\tan \beta }{1-\tan \alpha \cdot \tan \beta }}$

Tenim, doncs, la fórmula de la tangent d'una suma d'angles:

Exercici:

• Raons trigonomètriques de l'angle suma

Comencem trobant l'expressió que ens permeti desenvolupar el cosinus d'una resta d'angles, és a dir, donats dos angles $\alpha$ i $\beta$ , volem trobar $\cos (\alpha -\beta )$. En aquest cas ho farem transformant la resta en suma i utilitzant les expressions que ja coneixem de la suma.

$\cos (\alpha -\beta )=\cos (\alpha +(-\beta ))=\cos \alpha \cdot \cos (-\beta )-\sin \alpha \cdot \sin (-\beta )=$

i utilitzant relacions que ja coneixem:

$=\cos \alpha \cdot \cos \beta -\sin \alpha \cdot (-\sin \beta )=\cos \alpha \cdot \cos \beta +\sin \alpha \cdot \sin \beta$

Ja tenim, doncs, la fórmula del cosinus d'una resta d'angles:

Raonant de forma semblant podrem trobar la fórmula del sinus d'una resta d'angles. Fixa't:

$\sin (\alpha -\beta )=\sin (\alpha +(-\beta ))=\sin \alpha \cdot \cos (-\beta )+\cos \alpha \cdot \sin (-\beta )=$

i utilitzant relacions que ja coneixem:

$=\sin \alpha \cdot \cos \beta +\cos \alpha \cdot (-\sin \beta )=\sin \alpha \cdot \cos \beta -\cos \alpha \cdot \sin \beta$

Tenim, doncs, la fórmula del sinus d'una resta d'angles:

Fem el mateix per a la fórmula de la tangent:

$\tan (\alpha -\beta )=\tan (\alpha +(-\beta ))={\displaystyle \frac{\tan \alpha +\tan (-\beta )}{1-\tan \alpha \cdot \tan (-\beta )}}=$

i utilitzant relacions que ja coneixem:

$={\displaystyle \frac{\tan \alpha +(-\tan \beta )}{1-\tan \alpha \cdot (-\tan \beta )}}={\displaystyle \frac{\tan \alpha -\tan \beta }{1+\tan \alpha \cdot \tan \beta }}$

Tenim, doncs, la fórmula de la tangent d'una resta d'angles:

Exercici:

• Raons trigonomètriques de l'angle resta

Comencem trobant l'expressió que ens permeti desenvolupar el cosinus de l'angle doble, és a dir, donat un angle $\alpha$, volem trobar $\cos (2\alpha )$. Ho farem transformant el doble en suma i utilitzant les expressions que ja coneixem de la suma.

$\cos (2\alpha )=\cos (\alpha +\alpha )=\cos \alpha \cdot \cos \alpha -\sin \alpha \cdot \sin \alpha ={\cos }^2\alpha -{\sin }^2\alpha$

Ja tenim, doncs, la fórmula del cosinus de l'angle doble:

Raonant de forma semblant podrem trobar la fórmula del sinus de l'angle doble. Fixa't:

$\sin (2\alpha )=\sin (\alpha +\alpha )=\sin \alpha \cdot \cos \alpha +\cos \alpha \cdot \sin \alpha =2\cdot \sin \alpha \cdot \cos \alpha$

Tenim, doncs, la fórmula del sinus de l'angle doble:

Fem el mateix per a la fórmula de la tangent:

$\tan (2\alpha )=\tan (\alpha +\alpha )={\displaystyle \frac{\tan \alpha +\tan \alpha }{1-\tan \alpha \cdot \tan \alpha }}={\displaystyle \frac{2\tan \alpha }{1-{\tan }^2\alpha }}$

Tenim, doncs, la fórmula de la tangent de l'angle doble:

Exercici:

• Raons trigonomètriques de l'angle doble

El que volem trobar ara és l'expressió que ens permeti desenvolupar el cosinus de l'angle meitat, és a dir, donat un angle $\alpha$, volem trobar $\cos {\displaystyle \frac{\alpha }{2}}$. Ho farem a partir de relacions que ja coneixem. A l'apartat anterior hem vist que:

$\cos (2\alpha )={\cos }^2\alpha -{\sin }^2\alpha$

I això és vàlid per a qualsevol angle, en particular, també ho serà per a l'angle ${\displaystyle \frac{\alpha }{2}}$

$\cos \alpha ={\cos }^2{\displaystyle \frac{\alpha }{2}}-{\sin }^2{\displaystyle \frac{\alpha }{2}}$

Per altra banda, l'angle ${\displaystyle \frac{\alpha }{2}}$ complirà, com tots els angles, la relació fonamental de la trigonometria

$1={\cos }^2{\displaystyle \frac{\alpha }{2}}+{\sin }^2{\displaystyle \frac{\alpha }{2}}$

Sumant membre a membre aquestes dues darreres igualtats obtenim:

$1+\cos \alpha =2{\cos }^2{\displaystyle \frac{\alpha }{2}}$

I d'aquí obtenim:

${\cos }^2{\displaystyle \frac{\alpha }{2}}={\displaystyle \frac{1+\cos \alpha }{2}}⟶\cos {\displaystyle \frac{\alpha }{2}}=\pm \sqrt{{\displaystyle \frac{1+\cos \alpha }{2}}}$

Tenim, doncs, la fórmula del cosinus de l'angle meitat:

Tornem a les igualtats que abans hem sumat. Si, ara, a la segona li restem la primera obtenim:

$1-\cos \alpha =2{\sin }^2{\displaystyle \frac{\alpha }{2}}$

I d'aquí tenim:

${\sin }^2{\displaystyle \frac{\alpha }{2}}={\displaystyle \frac{1-\cos \alpha }{2}}⟶\sin {\displaystyle \frac{\alpha }{2}}=\pm \sqrt{{\displaystyle \frac{1-\cos \alpha }{2}}}$

Tenim, doncs, la fórmula del sinus de l'angle meitat:

Per fer la tangent:

$\tan {\displaystyle \frac{\alpha }{2}}={\displaystyle \frac{\sin {\displaystyle \frac{\alpha }{2}}}{\cos {\displaystyle \frac{\alpha }{2}}}}={\displaystyle \frac{\pm \sqrt{{\displaystyle \frac{1-\cos \alpha }{2}}}}{\pm \sqrt{{\displaystyle \frac{1+\cos \alpha }{2}}}}}=\pm \sqrt{{\displaystyle \frac{{\displaystyle \frac{1-\cos \alpha }{2}}}{{\displaystyle \frac{1+\cos \alpha }{2}}}}}=\pm \sqrt{{\displaystyle \frac{1-\cos \alpha }{1+\cos \alpha }}}$

Tenim, doncs, la fórmula de la tangent de l'angle meitat:

És important que te n'adonis que aquestes fórmules no determinen el signe del valor de la raó trigonomètrica. Hem de ser nosaltres els que, coneixent el quadrant al que pertany l'angle $\alpha$, esbrinem el quadrant al que pertany l'angle ${\displaystyle \frac{\alpha }{2}}$ i amb això determinem el signe de la raó trigonomètrica corresponent.

Exercici:

• Raons trigonomètriques de l'angle meitat

Resoldre un triangle vol dir arribar a conèixer tots els seus elements, és a dir, els tres costats a, b i c, i els tres angles A, B i C.

Per poder resoldre un triangle hem de conèixer tres dels seus elements, entre els quals com a mínim hi ha d'haver un costat.

En un triangle qualsevol es compleix:

• La suma dels tres angles val ${180}^{\circ }$. Figura 1 . No hi pot haver, per tant, més d'un angle obtús.
• Cadascun dels costats és més petit que la suma dels altres dos. Figura 2 .
• Al costat més gran s'hi oposa l'angle més gran; i al costat més petit, s'hi oposa l'angle més petit. Figura 3 .
• Teorema del cosinus
• Teorema dels sinus

Mou els vèrtexs del triangle i observa que sempre la suma dels angles és 180º.

Modifica els valors de a, b i/o c i observa què passa si un costat és més gran o igual que la suma dels altres dos.

Mou els vèrtexs del triangle i comprova que al costat més petit s'hi oposa l'angle més petit i al costat més gran, l'angle més gran.

$a^2=b^2+c^2-2\mathrm{bc}\cdot \cos A$

$b^2=a^2+c^2-2\mathrm{ac}\cdot \cos B$

$c^2=a^2+b^2-2\mathrm{ab}\cdot \cos C$

En aquest cas hem de trobar els tres angles A, B i C. La solució és única sempre que cada costat sigui més petit que la suma dels altres dos.

Exercici:

• Resoldre un triangle coneguts els tres costats

En aquest cas les dades conegudes venen donades per lletres diferents. Per exemple a, b, C.

Sempre trobarem una única solució.

Exercici:

• Resoldre un triangle coneguts dos costats i l'angle que formen
• Avió de reconeixement

Si ens donen un costat i dos angles, el problema té solució única sempre que els dos angles sumin menys de 180º.

Si ens donessin un costat i els tres angles caldrà mirar si els angles sumen 180º. Si no fos així, el problema no tindria solució.

Exercici:

• Resoldre un triangle coneguts un costat i dos angles
• Longitud d'un pal
• Rescat d'un nen
• Helicòpter
• Distància d'una regata
• Disseny d'un pont
• Localització d'un foc

Aquest cas és el més complicat. Ens podem trobar amb situacions on no hi ha cap triangle possible, que n'hi hagi un sol o que n'hi hagi dos.

Així trobarem problemes sense solució, amb una única solució o amb dues solucions.

És interessant que juguis una mica amb diferents costats i diferents angles.

Exercici:

• Resoldre un triangle coneguts dos costats i l'angle oposat a un d'ells
• Resoldre un triangle coneguts dos costats i l'angle oposat a un d'ells
• Resoldre un triangle coneguts dos costats i l'angle oposat a un d'ells
• Disseny d'un avió de combat

1. Angles
2. Mesurar angles en graus
3. Mesurar angles en radians
4. Equivalència entre graus i radians
5. Mesura principal d'un angle
6. Raons trigonomètriques d'un angle agut
7. Resolució de triangles rectangles
8. Raons trigonomètriques d'un angle qualsevol
9. Línies trigonomètriques
10. Reducció al primer quadrant
    • Angle del 2n quadrant
    • Angle del 3r quadrant
    • Angle del 4t quadrant
11. Relació entre les raons trigonomètriques d'angles oposats
12. Relació entre les raons trigonomètriques d'angles complementaris
13. Raons trigonomètriques dels angles importants
14. Relacions entre les raons trigonomètriques d'un mateix angle
15. Fórmules d'addició
    • Raons trigonomètriques d'una suma d'angles
    • Raons trigonomètriques d'una resta d'angles
    • Raons trigonomètriques de l'angle doble
    • Raons trigonomètriques de l'angle meitat
16. Resolució de triangles obliquangles
    • Coneguts els tres costats
    • Coneguts dos costats i l'angle que formen
    • Coneguts un costat i dos o tres angles
    • Coneguts dos costats i l'angle oposat a un d'ells