OEF Polynômes
--- Introduction ---
Ce module regroupe pour l'instant 32 exercices sur les polynômes à une
variables (avec coefficients réels ou complexes) : racines, degrés,
composition, division euclidienne, ...
Degré du pgcd avec dérivée
Soit
un polynôme de degré et à coefficients , ayant racines réelles et racines complexes différentes (non comptées avec multiplicités). Soit
la dérivée de
. Quel est le degré de pgcd(
) ?
Min. deg racines multiples
Quel est le degré minimum d'un polynôme P(x) à coefficients admettant : - comme racine de multiplicité ;
- comme racine de multiplicité ?
Répondez -1 si vous pensez qu'un tel polynôme n'existe pas.
Degré de somme
Soient () et () deux polynômes. Complétez : Si deg()= et deg()=, alors est un polynôme de degré ________.
Equation de différence
Trouver le polynôme () tel que ()-() = 2 et que ()=.
Tapez x^3 pour 3, etc.
Trouver racine multiple degré 3
Le polynôme suivant a une racine multiple. Trouver cette racine.
Trouver racine multiple degré 4
Le polynôme suivant a une racine multiple. Trouver cette racine.
Trouver racine multiple degré 5
Le polynôme suivant a une racine multiple. Trouver cette racine.
Trouver racine multiple degré 6
Le polynôme suivant a une racine multiple. Trouver cette racine.
pgcd donné avec dérivée
Trouver le polynôme
tel que : - pgcd(
) =
, où
est le polynôme dérivé de
;
-
;
- le degré de
est le plus petit possible.
Vous pouvez entrer le polynôme sous forme développée ou factorisée. Tapez x^3 pour
, etc.
Racine donnée deg 3
Déterminez le polynôme P() = 32 , sachant que et sont réels, et que en est une racine.
Min. deg pgcd avec dérivée 2
Soit P(x) un polynôme de degré et à coefficients , ayant racines réelles et racines complexes différentes (non comptées avec multiplicités). Soit P''(x) la dérivée seconde de P(x). Quel est le minimum du degré de pgcd(P(x),P''(x)) ?
Min. deg pgcd avec dérivée n
Soit P(x) un polynôme de degré et à coefficients , ayant racines réelles et racines complexes différentes (non comptées avec multiplicités). Soit P()(x) la dérivée d'ordre de P(x). Quel est le minimum du degré de pgcd(P(x),P()(x)) ?
Multiplicité d'une racine degré 3
Le nombre est une racine du polynôme suivant. Calculer sa multiplicité.
Multiplicité d'une racine degré 4
Le nombre est une racine du polynôme suivant. Calculer sa multiplicité.
Multiplicité d'une racine degré 5
Le nombre est une racine du polynôme suivant. Calculer sa multiplicité.
Multiplicité d'une racine degré 6
Le nombre est une racine du polynôme suivant. Calculer sa multiplicité.
Multiplicité paramétrée degré 3
Trouver une valeur de
pour que le polynôme suivant ait une racine multiple, et trouver cette racine multiple.
ATTENTION. Cet exercice n'accepte pas les réponses approximatives ! Il y a toujours une solution entière. Trouvez-la.
Multiplicité paramétrée degré 4
Trouver une valeur de
pour que le polynôme suivant ait une racine multiple, et trouver cette racine multiple.
ATTENTION. Cet exercice n'accepte pas les réponses approximatives ! Il y a toujours une solution entière. Trouvez-la.
Paramétré deg 2
Pour quelles valeurs réelles du paramètre le polynôme ()2 + (2) + a ? (
)
Paramétré deg 2 II
Pour quelle valeur réelle du paramètre le polynôme ()2 + () + () a une racine égale à ? (Sous condition que 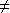 0.)
0.)
Racines polynome complexe deg 2
Calculer les deux racines du polynôme P() = 2 + () + (). Vous pouvez entrer les deux racines , dans n'importe quel ordre.
Fonction de racines deg 2
Soient
,
les deux racines du polynôme
où
est un coefficient réel. Quelle est la valeur de
? (Cette valeur est une fonction de
.)
Fonction de racines deg 3
Soient
,
,
les trois racines du polynôme
, où
est un coefficient réel non nul. Quelle est la valeur de
? (Cette valeur est une fonction de a.)
Re(racine) deg 2
Soit P() = 2 + un polynôme à coefficients réels, ayant deux racines complexes conjuguées. Quelle est la partie réelle d'une racine r ?
Compte racines avec dérivée
Soit
un polynôme de degré et à coefficients , et soit
le polynôme dérivé de
. On sait que pgcd(
) est un polynôme de degré . Quel est le nombre de racines distinctes de
? (racines réelles et complexes confondues)
Racine de polynôme composé
Soient () un polynôme, et () = 2 un autre polynôme. Considérons les polynômes composés (()) et (()). Complétez : Si est une racine de , alors .
Racines réelles deg 2
Trouver les deux racines r1, r2 du polynôme 2 . (Les racines sont réelles, et l'ordre des racines est sans importance.)
Multiplicité racine de somme
Soient () et () deux polynômes. Complétez : Si est une racine de multiplicité de () et aussi une racine de multiplicité de (), alors est une racine de multiplicité ________ de .
Statut racines deg 2
Quel est le type de racines du polynôme de degré 2 suivant ? 2
Factorisation de trinôme
Factoriser
.
Etape 1. Mettons les termes de
en un carré complet :
= (
)2.
Nous avons
.
Etape 2. Donc
Donc
Etape 3.
Maintenant on applique la formule
(
)(
).
Résultat :
.
(Il faut entrer les expressions simplifiées.)
Racine triple deg 3
Pour quelles valeurs réelles des paramètres et le polynôme P() = 3 + 2 + + (-) a une racine triple ?
Racine triple deg 3 II
Pour quelles valeurs réelles des paramètres et le polynôme P() = 3 2 +(++) a une racine triple ? (La solution n'est pas forcément unique.)
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les polynômes d'une variable (coefficients réels ou complexes). interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, algebra, polynomials,roots,gcd_lcm,complex_number
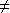 0.)
0.)
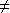 0.)
0.)