Ensembles
Objectifs et conseils
Ce module est consacré à la théorie des ensembles. Nous revenons aussi sur les propriétés des applications.
Références
- F. Liret et D. Martinais, Mathématiques pour le DEUG, Algèbre 1ère Année (Dunod), chapitre 1
- Annick Auzimour et Frédérique Petit, Travaux dirigés d'algèbre (Vuibert).
- Anne Denmat et Françis Héaulme, Algèbre générale (Dunod).
Guide
Union, intersection, complémentaire
- Union, intersection, complémentaire : définitions
- Associativité et distributivité
- Quelques problèmes concrets
Union, intersection, complémentaire : définitions
Inclusion : Un ensemble est inclus (contenu) dans un ensemble si tout élément de est un élément de . Cela est noté E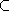 F.
F.
Les trois opérations de la théorie des ensembles sont
- la
réunion,
La réunion de deux sous-ensembles et d'un ensemble W est l'ensemble des éléments de qui appartiennent à ou à . Elle est notée E
 F :
F :
- l'
intersection,
L'intersection de deux sous-ensembles E et F d'un ensemble W est l'ensemble des éléments de W qui appartiennent à la fois à E et à F. Elle est notée E
 F
F
- le
complémentaire,
Si est un sous-ensemble de , le complémentaire de E dans F est l'ensemble des éléments de qui n'appartiennent pas à . Il est noté c ou ou .
- la
différence symétrique,
La différence symétrique de deux sous-ensembles et d'un ensemble est l'ensemble des éléments de qui appartiennent à et non à ou qui appartiennent à et non à . Elle est notée
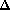 .
.
On a donc
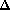 F = (
F = (
 ) - (
) - (
 ) = (
-
)
) = (
-
)  (
-
)
(
-
)
Il est important de bien comprendre graphiquement de quoi il s'agit. Par exemple, si on vous donne trois sous-ensembles , et , savez-vous reconnaître ou ?
- soit présenter un sous-ensemble graphiquement et vous demander de reconnaitre la formule correspondante : série 1 ou série 2
- ou donner une formule à partir des opérations d'union, d'intersection et de complémentaire et vous demander de le reconnaitre graphiquement Sous-ensembles graphiques
Associativité et distributivité
Il faut savoir manipuler les expressions contenant des symboles union, réunion, complémentaire. Les lois essentielles sont-
l'associativité
Si , et sont deux sous-ensembles de , on a
-
la distributivité entre l'union et l'intersection
Si , et sont deux sous-ensembles de , on a
Quelques problèmes concrets
Jean s'occupe des livres politiques et des romans étrangers reliés ;
Pierre s'occupe des livres politiques reliés et des romans anglais, sauf ceux qui sont politiques ;
Henri s'occupe des livres anglais et des romans politiques non reliés.
Quels sont les livres qui sont de la compétence des trois employés ? de deux ? d'aucun ? Mettre le problème sous forme mathématique. On peut aussi faire un dessin !
Cardinal
Cardinal
On ne considère que des ensembles finis et on note Card le cardinal de , c'est-à-dire le nombre d'éléments de . La formule fondamentale pour le calcul des cardinaux est :
 ) = Card (
) + Card (
) - Card (
) = Card (
) + Card (
) - Card (
 )
)
 B )= card(A) + card(B) - card(A
B )= card(A) + card(B) - card(A B)
B)
Donner un majorant de Card (
 ) en fonction de
,
et
. Même question pour Card (
) en fonction de
,
et
. Même question pour Card (
 ).
).
Donner un minorant de Card (A  B) en fonction de
,
et
. Même question pour Card (
B) en fonction de
,
et
. Même question pour Card (
 ).
).
 B)
B) 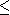 Inf(a+b,n)
Inf(a+b,n) B)
B) 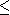 b
b B)
B) 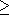 a
a
 B)
B) 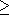 Sup(0,a+b-n)
Sup(0,a+b-n)

 )
)
 B
B  C) =
Card( A )+ Card (B) + Card (C)
- Card (A
C) =
Card( A )+ Card (B) + Card (C)
- Card (A
 B)
B)
- Card (A
 C)-Card (C
C)-Card (C  B)
+Card (A
B)
+Card (A  B
B  C)
C)
Cardinaux : exercices pratiques
Applications
Bijectivité, injectivité, surjectivité (ensembles finis)
Bijectivité sur R
 dans
dans  , que peut-on dire de
l'image d'un ensemble borné, de son image réciproque ? Attention aux
pièges
!
, que peut-on dire de
l'image d'un ensemble borné, de son image réciproque ? Attention aux
pièges
!
- Des questions sur une "fonction quadratique" sont posées : définition, injectivité, surjectivité. On peut s'aider d'un calculateur graphique : OEF Fonctions réciproques
- Calculer l' image réciproque d'un intervalle par une fonction f quadratique. Aide
- Comparer f(f-1(I)) et I pour I un intervalle.
- Comparer f-1(f(I)) et I pour I un intervalle.
Image réciproque d'un intervalle
Les situations qui peuvent apparaître sont les suivantes pour une parabole :
L'image réciproque de l' intervalle bleu (vertical) est l'ensemble orange (horizontal). Il est donc selon les cas vide, un intervalle, la réunion disjointe de deux intervalles. En particulier, ce n'est pas toujours un intervalle.
Pour faire l'exercice en ligne, utilisez la calculette graphique ou votre calculette.