Ensembles
--- Introduction ---
Ce module regroupe pour l'instant 18 exercices
sur les ensembles, le cardinal d'un ensemble, la représentation d'événements par des ensembles et les applications entre deux ensembles finis.
Le paramètre "Complexité des ensembles" sert uniquement pour les exercices Positions de points aléatoires,
Cardinal d'un ensemble classique, Cardinal d'un sous-ensemble du plan et
Description d'un sous-ensemble du plan.
Distance de Manhattan
Une personne se trouve au numéro de la ème avenue. Il désire prendre un taxi pour se rendre au numéro de la ème avenue.
On suppose que les avenues de Manhattan sont quadrillées de telle sorte que le taxi peut changer d'avenue tous les 10 numéros et on suppose que le compteur du taxi avance d'un dollar à chaque croisement. -
Combien coûtera la course si le taxi est honnête ?
Bonne réponse ! La course coûtera dollars. - Combien de fois le taxi peut-il faire cette course sans emprunter le même trajet (en supposant toujours que le chauffeur est honnête) ?
Répartition d'élèves dans des options
Sur les élèves d'un lycée, suivent des cours d'anglais, ceux d'allemand, ceux d'espagnol. Parmi eux, apprennent au moins l'anglais et l'espagnol, apprennent au moins l'anglais et l'allemand et apprennent au moins l'allemand et l'espagnol. Enfin, d'entre eux apprennent les trois langues.
- Combien n'apprennent aucune de ces trois langues ?
- Combien d'élèves font uniquement de l'anglais et de l'espagnol ?
Comparer deux ensembles
On considère les deux ensembles suivants :
Dénombrabilité
L'ensemble
est-il dénombrable ?
Description d'un sous-ensemble du plan
On note
l'ensemble
E =
- Comme sous-ensemble du plan, les éléments de
constituent tous les points à coordonnées entières inclus dans
.
.
- Une autre façon d'écrire l'ensemble
est :
=
(x,
)
tel que
x
-
Pour tout entier
vérifiant
, l'ensemble
(x,y) tel que x
et
x
a
éléments.
Le cardinal de
est
.
- Le cardinal de
est
.
Ecriture ensembliste d'événements
On effectue une expérience aléatoire dont l'ensemble des résultats est noté
. On désigne par
et
deux événements qui peuvent se réaliser au cours de cette expérience. Par abus de notations,
et
désignent aussi les parties de
qui décrivent ces événements : par exemple, si
est le résultat de l'expérience, il est équivalent de dire que
est réalisé et que
. Quelle est l'écriture ensembliste de l'événement
suivant ?
=
.
Théorie des ensembles 1
Soit
un ensemble et
,
et
trois sous-ensembles de
. Traduire en termes mathématiques la phrase suivante : L'ensemble
des éléments de
qui
qui
.
Points à coordonnées entières
On considère l'ensemble
des couples
tels que
et
et tels que
.
Evénements et ensembles
On effectue une expérience aléatoire dont l'ensemble des résultats est noté
. On désigne par
,
et
trois événements qui peuvent se réaliser au cours de cette expérience. Par abus de notations,
,
et
désignent aussi les parties de
qui décrivent ces événements : par exemple, si
est le résultat de l'expérience, il est équivalent de dire que
est réalisé et que
. - Quelle est l'écriture ensembliste de l'événement
suivant :
Bonne réponse, l'événement
est représenté par l'ensemble .
- Quel est l'événement complémentaire
?
Bonne réponse, l'événement complémentaire
est
- Quelle est l'écriture ensembliste de l'événement complémentaire
?
Fonctions indicatrices
. Donner l'expression de la fonction indicatrice de l'ensemble
au point
, en notant
et
.
=
Injectivité, surjectivité
Soient
et
deux ensembles finis tels que card
card
.
. (La réponse autre signifie qu'aucune des propositions n'est possible.)
Positions de points aléatoires
On a choisi au hasard à l'intérieur du dessiné en marron, centré en 0 et dont le mesure mm. l'événement .
line 221,100,241,100,blue line 221,99,221,101,blue line 231,99,231,101,blue line 241,99,241,101,blue text navy,220,85,medium, 20 mm arrow 0,110,220,110,10,gray arrow 110,220,110,0,10,gray text gray, 100,110,,0 linewidth 3 points navy,
L'événement est-il réalisé ?
Cardinal d'un ensemble classique
Quel est le cardinal de l'ensemble E suivant ? E =
Cardinal d'un sous-ensemble du plan
Quel est le cardinal de l'ensemble E suivant ? E =
Associer événements et ensembles
On effectue une expérience aléatoire dont l'ensemble des résultats est noté
. On désigne par
,
et
trois événements qui peuvent se réaliser au cours de cette expérience. Par abus de notations,
,
et
désignent aussi les parties de
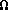
qui décrivent ces événements : par exemple, si
est le résultat de l'expérience, il est équivalent de dire que
est réalisé et que
.
Ensembles : description mathématique
Soit
,
et
trois ensembles. La colonne de droite contient les descriptions des éléments de quatre ensembles différents. Lesquels ?
Associer l'ensemble correspondant à chaque description.
Description des éléments d'un ensemble
Soit
,
et
trois ensembles. Faire correspondre les affirmations équivalentes.
Ensembles de multiples
Soit
l'ensemble des entiers de 1 à multiples de . Soit
le sous-ensemble de
formé des multiples de et
le sous-ensemble de
formé des multiples de .
Donner explicitement la liste
des éléments (si
est vide, écrire 0).
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les ensembles, les événements et les applications entre deux ensembles finis. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, mathematics, discrete_mathematics, probability, events, set_theory, maps, combinatorics
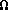 qui décrivent ces événements : par exemple, si
est le résultat de l'expérience, il est équivalent de dire que
est réalisé et que
.
qui décrivent ces événements : par exemple, si
est le résultat de l'expérience, il est équivalent de dire que
est réalisé et que
.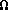 qui décrivent ces événements : par exemple, si
est le résultat de l'expérience, il est équivalent de dire que
est réalisé et que
.
qui décrivent ces événements : par exemple, si
est le résultat de l'expérience, il est équivalent de dire que
est réalisé et que
.