OEF subspace definition
--- Introduction ---
This module actually contains 21 exercises on the definition of
subspaces of vector spaces.
You are given a vector space and a subset defined in various ways;
up to you to determine whether the subset is a subspace.
See also the collections of exercises on
vector spaces in general or
defition of vector spaces.
Continuous functions
Let
be the
-vector space of real functions
, and let
be the subset of
composed of the function 0 and functions which are on [,].
Is
a subspace of
?
Increasing functions
Let
be the
-vector space of real functions
, and let
be the subset of
composed of the function 0 and functions which are on [,].
Is
a subspace of
?
Crossed Matrices
Let
be the vector space of matrices of size
, and let
be the subset of
composed of matrices
such that
Is
a subspace of
?
Matrices and determinant
Let
be the vector space of matrices of size ×, and let
be the subset of
composed of matrices M whose is equal to . Is
a subspace of
?
Matrices and elements
Let
be the vector space of matrices of size ×, and let
be the subset of
composed of matrices M such that . Is
a subspace of
?
Multiplied matrices
Let
be the vector space of matrices of size
, and let
be the subset of
composed of matrices
. Is
a subspace of
?
Matrices and rank
Let
be the vector space of matrices of size ×, and let
be the subset of
composed of matrices of rank . Is
a subspace of
?
You must give all the good replies.
Matrices with power
Let
be the vector space of matrices of size ×, and let
be the subset of
composed of matrices M such that M=0. Is
a subspace of
?
Periodic functions
Let
be the vector space of real continuous functions over
, and let
be the subset of
composed of the function 0 and periodic functions whose period . Is
a subspace of
?
Polynomials and coefficients
Let
be the
-vector space of real polynomials P(X) of degree less than or equal to , and let
be the subset of
composed of polynomials such that the of its coefficients equals . Is
a subspace of
?
Polynomials and degrees
Let
be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
with degree . Is
a subspace of
?
Polynomials and integral
Let
be the vector space over
of polynomials, and let
be the subset of
composed of polynomials
such that
Is
a subspace of
?
Polynomials and integral II
Let
be the vector space over
of polynomials, and let
be the subset of
composed of polynomials
such that
Is
a subspace of
?
Polynomials and roots
Let
be the
-vector space of real polynomials P(X) of degree less than or equal to , and let
be the subset of
composed of polynomials such that the of its roots (real or complex, counted with multiplicity) equals 0. Is
a subspace of
?
Polynomials and roots II
Let
be the
-vector space of real polynomials P(X) of degree less than or equal to , and let
be the subset of
composed of polynomials with . Is
a subspace of
?
Polynomials and values
Let
be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
such that
. Is
a subspace of
?
Polynomials and values II
Let
be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
(X) such that
. Is
a subspace of
?
Polynomials and values III
Let
=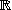 [X] be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
such that
.
[X] be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
such that
. Is
a subspace of
?
Real functions
Let
be the
-vector space of real functions
, and let
be the subset of
composed of functions
(x) .
Is
a subspace of
?
Square matrices
Let
be the vector space of matrices of size ×, and let
be the subset of
composed of matrices. Is
a subspace of
?
Vectors of R^3
Let
be the vector space of dimension 3 over
, and let
be the subset of
composed of vectors
such that
. Is
a subspace of
?
The most recent version
Esta página no tiene el aspecto habitual porque WIMS no ha podido reconocer
su navegador web.
Por favor, observe que las páginas de WIMS se generan interactivamente; no son
archivos HTML ordinarios. Deben usarse interactivamente y estando conectados. Es inútil
que las almacene con un programa automático.
- Description: collection of exercices on the definition of subspace of vector spaces. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, algebra, linear algebra, vector space, subspace, polynomial, matrix, function
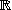 [X] be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
such that
.
[X] be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
such that
.