Changement de variables
Objectifs
La méthode du changement de variable est très utile pour le calcul d'intégrale ou de primitive ; elle peut conduire à des erreurs si elle n'est pas appliquée avec soin. On peut aussi se compliquer la vie inutilement si on l'applique de travers.
Guide
Le théorème
 une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
Cas où le changement de variables est évident
On doit calculer ; on voit que apparaît toujours par l'intermédiaire d'une expression plus complexe et de sa dérivée : une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
 est
sur [a,b] et on remplace
est
sur [a,b] et on remplace
| par | ||
| par | ||
| les bornes et | par | et . |
On obtient ainsi une nouvelle intégrale égale à l'intégrale .
Remarque : Quand vaut , la nouvelle variable vaut ...
Exemple
Pour voir le théorème en même temps.
 une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
Calculons . La fonction à intégrer est de la forme où est la dérivée de et où est la fonction définie par . On fait donc le changement de variable :
- On prend et .
-
On vérifie que
 est une fonction
sur l'intervalle [2 ,4].
est une fonction
sur l'intervalle [2 ,4].
- On vérifie que est une fonction continue sur l'intervalle .
- Puis on remplace
par par les bornes 2 et 4 par et
On obtient donc :
Cas où le changement de variables n'est pas évident
On peut aussi utiliser la formule du théorème une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
Contrairement à ce qu'il est souvent écrit, on n'a pas besoin de définir la fonction réciproque de  . Par contre, il est essentiel de trouver un intervalle [a,b] tel que
. Par contre, il est essentiel de trouver un intervalle [a,b] tel que
- la fonction
 est définie, de classe
sur [a,b] et vérifie
et
est définie, de classe
sur [a,b] et vérifie
et
- la fonction est continue sur (attention, peut être plus grand que ).
On peut alors appliquer le théorème
 une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
 :
:
- on choisit et vérifiant et et on détermine l'intervalle ;
- on vérifie que
 est
sur l'intervalle [a,b] ;
est
sur l'intervalle [a,b] ;
- on vérifie que est une fonction continue sur ; c'est immédiat dans le cas ;
- on remplace
par par les bornes  et
et
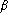
par et
On obtient ainsi une nouvelle intégrale égale à l'intégrale .
Remarque :
- En général, on choisit
et
de manière à ce que la fonction
 soit bijective de [a,b] sur [
soit bijective de [a,b] sur [ ,
,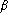 ], et en particulier tel que
soit égal à
: par exemple dans le cas où le changement de variables est x=cos(u) avec les bornes
et
, personne n'aurait l'idée saugrenue de prendre
et
si la fonction
est définie sur
], et en particulier tel que
soit égal à
: par exemple dans le cas où le changement de variables est x=cos(u) avec les bornes
et
, personne n'aurait l'idée saugrenue de prendre
et
si la fonction
est définie sur  . Mais c'est permis !
. Mais c'est permis !
- En aucun cas, il n'est nécessaire que la réciproque de
 soit
.
soit
.
Exemple typique Exercices corrigés
Exemple typique
Pour voir le théorème. une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
une fonction réelle de classe
définie sur l'intervalle [a,b]. Soit
une fonction continue sur l'intervalle
. On a l'égalité :
On veut calculer l'intégrale
.
On a envie de poser
et de prendre comme fonction
 la fonction définie par
sur un intervalle à déterminer.
la fonction définie par
sur un intervalle à déterminer.
- La fonction
 est
sur
est
sur  . On choisit deux nombres
et
tel que
. On choisit deux nombres
et
tel que et , et par exemple.,On peut aussi prendre et ; mais bien sûr, jamais personne ne fera cela !L'image de est de toute façon contenue dans [-1,1] (et même égale).
- La fonction définie sur [-1,1] par est continue sur [-1,1] ;
-
On obtient par le théorème :
Sur l'intervalle [0, ], la fonction sin est positive, on a donc :
], la fonction sin est positive, on a donc :
Remarquons que si on avait pris les bornes saugrenues et , la fonction sin n'aurait pas été positive entre et et le calcul aurait été moins simple !
Exercices corrigés
- la fonction définie sur l'intervalle [ ] par est .
-
Son image est contenue dans l'intervalle [-1,1]. On a
, - La fonction définie sur [-1,1] par est continue sur [-1,1].
Bien que correct, le choix de cet intervalle est tout à fait déconseillé car la suite des calculs serait très compliquée puisqu'il faudrait séparer en intervalles où est de signe constant pour calculer .
- la fonction est définie et sur l'intervalle [a,b] (ou [b,a]).
Par contre en transformant astucieusement, on peut utiliser dans ce cas le changement de variable dit évident
ou conseillé, c'est-à-dire transformer 1/(2+cos(x)) par les formules de trigonométrie jusqu'à tomber sur
une expression de la forme
.
Sur quel intervalle peut-on alors prendre comme fonction
 la fonction donnée par
?
la fonction donnée par
?
Changement de variables dans une primitive
Pour le calcul de la primitive sur l'intervalle [c,d] (avec ), on applique le changement de variable si on peut- choisir un vérifiant et un tel que
- vérifier que
 est
sur
(ou
)
est
sur
(ou
)
- vérifier que est une fonction continue sur .
Pour remplir ces conditions, on est donc amené à choisir un changement de variable
 bijectif sur [c,d] afin de pouvoir considérer la fonction réciproque
bijectif sur [c,d] afin de pouvoir considérer la fonction réciproque
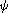 de
de
 sur
.
sur
.
- pour tout x de [c,d], on pose y=
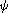 (x)
(x)
- on vérifie que
 est
sur
est
sur
- on vérifie que est continue sur [c,d].
La primitive est alors définie sur [c,d] et on a en tout point de [c,d]
Exercices interactifs