OEF sequences
--- Introduction ---
This module actually contains 16 exercises on infinite sequences:
convergence, limit, recursive sequences, ...
Two limits
Let () be an infinite sequence of real numbers. If one has and for , what can be said about its convergence? (You should choose the most pertinent consequence.)
Comparison of sequences
Let () and () be two sequences of real numbers where () converges towards . If one has , what can be said about the convergence of ()? (You must choose the most pertinent consequence.)
Growth and bound
Let () be a sequence of real numbers. If () is , what can be said about its convergence (after its existence)?
Convergence and difference of terms
Let be a sequence of real numbers. Among the following assertions, which are true, which are false? - If , then .
- If , then .
Convergence and ratio of terms
Let be a sequence of real numbers. Among the following assertions, which are true, which are false? - If , then .
- If , then .
Epsilon
Let be a sequence of real numbers. What does the condition imply on the convergence of ? (You must choose the most pertinent consequence.)
Fraction 2 terms
Compute the limit of the sequence (un), where
Fraction 3 terms
Compute the limit of the sequence (un), where
Fraction 3 terms II
Compute the limit of the sequence (un), where
WARNING IN this exercise, approximative replies will be considered as false! Type pi instead of 3.14159265, for example.
Growth comparison
What is the nature of the sequence (un), where
?
Monotony I
Study the growth, sup, inf, min, max of the sequence (un) for n 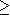 , where
.
, where
. Write for a value that does not exist, and or - for + or -
or - .
.
Monotony II
Study the growth, sup, inf, min, max of the sequence (un) for n 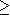 , where
.
, where
. Write for a value that does not exist, and or - for + or -
or - .
.
Powers I
Compute the limit of the sequence (un), where
Powers II
Compute the limit of the sequence (un), where
Type no if the sequence is divergent.
Recursive function
The sequence
such that
is a recursive sequence defined by
for a certain function
. Find this function.
Recursive limit
Find the limit of the recursive sequence
such that
The most recent version
This page is not in its usual appearance because WIMS is unable to recognize your
web browser.
Please take note that WIMS pages are interactively generated; they are not ordinary
HTML files. They must be used interactively ONLINE. It is useless
for you to gather them through a robot program.
- Description: collection of exercises on infinite sequences. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, analysis, calculus, sequence, limit, convergence
 or -
or - .
.
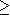 , where
, where  or -
or - .
.
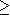 , where
, where  or -
or - .
.