OEF arithmétique modulaire
--- Introduction ---
Ce module regroupe pour l'instant 38 exercices sur les calculs sur
l'anneau fini  /n
/n .
.
Trous d'addition
Considérons une application
, qui envoie
sur
. Remplissez le tableau suivant pour
en tirant les nombres donnés en bas.
Classes de congruences
?
Congruences avec un paramètre
Calculer le nombre
modulo en fonction du chiffre
. Consigne : Dans la réponse, les entiers doivent être compris entre 0 et .
Trous cubiques
Considérons une application
, qui envoie
sur
. Remplissez le tableau suivant pour
en tirant les nombres donnés en bas.
Trous de division
Considérons une application
, qui envoie
sur
. Remplissez le tableau suivant pour
en tirant les nombres donnés en bas.
Division I
Calculer / . Le résultat doit être représenté par un nombre compris entre 0 et .
Division II
Calculer / . Le résultat doit être représenté par un nombre compris entre 0 et .
Division III
Calculer / . Le résultat doit être représenté par un nombre compris entre 0 et .
Diviseurs de zéro
Le nombre est-il un diviseur de zéro ?
Diviseurs de zéro II
Trouver l'ensemble des diviseurs de zéro . (Dans cet exercice on ne considère pas le 0 comme un diviseur de zéro.) Ecrire chaque élément par un nombre compris entre 1 et , et séparer les éléments par des virgules.
Diviseurs de zéro III
Soit = 2, où est un nombre premier. Combien de diviseurs de zéro y a-t-il ? Dans cet exercice, on ne considère pas le 0 comme un diviseur de zéro.
Racines modulo p^2
Soit le polynôme
. Il a deux racines
et
.
Les calculer
(on les donnera sous forme d'un entier compris entre 0 et ).
Soit
dans  .
.
Calculer
mod
.
(les entiers apparaissant seront compris entre 0 et
).
Vous avez trouvé
mod
.
Ainsi, l'équation
mod
est équivalente à
mod
.
Existe-t-il un unique entier
compris entre 0 et
, congru à modulo et tel que
mod
?
Réponse :
L'équation
mod
est en effet équivalente à l'équation
mod . Calculer l'entier
compris entre 0 et
, congru à modulo et tel que
mod
.
Combien y-a-t-il de solutions (modulo
) à l'équation
mod
qui soient congrues à mod ?
Inverse I
Trouver l'inverse de . Le résultat doit être représenté par un nombre compris entre 0 et .
Inverse II
Trouver l'inverse de . Le résultat doit être représenté par un nombre compris entre 0 et .
Inverse III
Trouver l'inverse de . Le résultat doit être représenté par un nombre compris entre 0 et .
Puissance inversible
est un nombre premier. La fonction
définie par
est-elle bijective ?
Divisibilité
On suppose que le nombre premier divise
pour deux entiers
et
. Peut-on conclure que divise
et
?
Equation linéaire modulaire
Soit l'équation dans 
 mod
mod
L'équation a-t-elle une solution ?
L'ensemble des solutions
est de la forme
 avec
un entier positif et
un ensemble fini d'entiers de
avec
un entier positif et
un ensemble fini d'entiers de 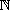 strictement inférieurs à
. En prenant
le plus petit possible, donner tous les éléments de
.
L'ensemble des solutions
est de la forme
strictement inférieurs à
. En prenant
le plus petit possible, donner tous les éléments de
.
L'ensemble des solutions
est de la forme
 avec
un ensemble fini d'entiers de
strictement inférieurs à . Donner tous les éléments de
.
avec
un ensemble fini d'entiers de
strictement inférieurs à . Donner tous les éléments de
.
+


Remplacer le second membre par un autre entier de manière à ce que la nouvelle équation ait une solution.
Trous de multiplication
Considérons une application
, qui envoie
sur
. Remplissez le tableau suivant pour
en tirant les nombres donnés en bas.
Multiples spéciaux
Soit
. Trouver le plus petit entier
tel que l'entier qui s'écrit en base
avec
chiffres tous égaux à 1 soit un multiple de
.
Multiples spéciaux II
Soit
. C'est un nombre premier. Trouver le plus petit entier
tel que l'entier qui s'écrit en base
sous la forme
avec
fois le motif soit un multiple de
.
Période d'un rationnel en base b
Le développement du rationnel
écrit en base est périodique de période à partir de la
première
-ième
"décimale". Quels sont tous les diviseurs premiers possibles du dénominateur de
(dans l'écriture décimale) ?
Trous de polynôme
Considérons une application
, qui envoie
sur
. Remplissez le tableau suivant pour
en tirant les nombres donnés en bas.
Puissances
Calculer l'élément . Le résultat doit être représenté par un nombre compris entre 0 et .
Puissances II
est un nombre premier. Calculez l'élément . Le résultat doit être représenté par un nombre compris entre 0 et .
Trous de puissance
Considérons une application
, qui envoie
sur
. Remplissez le tableau suivant pour
en tirant les nombres donnés en bas.
Racines modulo
Soit
le nombre premier . On désire calculer un entier
tel que
 mod .
mod .
- Calculer un entier
tel que
soit congru à 1 modulo un nombre
que vous devez déterminer et qui vous sera utile pour ce problème.
=
=
- Quelle puissance de
faut-il calculer ?
- Calculer une solution
=
mod .
Racines
est un nombre premier. Il existe un élément
, tel que a soit congru à modulo . Trouver
. Le résultat doit être représenté par un nombre compris entre 0 et .
Racines de l'unité modulo p (I)
Soit l'équation
 1 mod .
1 mod .
Calculer le plus petit entier
tel que cette équation soit équivalente à
 1 mod
1 mod
et donner le nombre de solutions.
Racines de l'unité modulo p (II)
Soit le système d'équations
Calculer le plus petit entier
tel que cette équation soit équivalente à
 1 mod .
1 mod .
Quel est le nombre de solutions modulo ?
Calculs simples dans Z/nZ
Calculer
dans  /
/ .
. Le résultat doit être représenté par un nombre compris entre 0 et .
Calculs simples modulo n
Calculer
modulo . Le résultat doit être représenté par un nombre compris entre 0 et .
Carrés
Trouver l'ensemble des carrés . Ecrire chaque élément par un nombre compris entre 0 et et séparer les éléments par des virgules.
Somme et produit
Trouver deux entiers
et
tels que
,
,
Vous pouvez entrer les deux nombres dans n'importe quel ordre.
Système linéaire modulo n II
Trouver toutes les solutions dans  du système d'équations suivant
du système d'équations suivant
On écrira les solutions sous la forme avec
et
dans  .
.
Système linéaire modulo n I
Le système d'équations suivant
a-t-il une unique solution modulo ?
Système linéaire modulo n II
Trouver toutes les solutions dans  du système d'équations suivant
du système d'équations suivant
On écrira les solutions sous la forme
=
+
*
+
*
=
+
*
+
*
avec
et
dans  .
.
Trous de trinôme
Considérons une application
, qui envoie
sur
. Remplissez le tableau suivant pour
en tirant les nombres donnés en bas.
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices dans l'anneau Z/nZ ou congruences modulo n. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, algebra,arithmetic, modular_arithmetic
 .
.
 /n
/n .
.
 .
.

 mod
mod  avec
un entier positif et
un ensemble fini d'entiers de
avec
un entier positif et
un ensemble fini d'entiers de 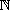 strictement inférieurs à
. En prenant
le plus petit possible, donner tous les éléments de
.
L'ensemble des solutions
est de la forme
strictement inférieurs à
. En prenant
le plus petit possible, donner tous les éléments de
.
L'ensemble des solutions
est de la forme
 avec
un ensemble fini d'entiers de
strictement inférieurs à . Donner tous les éléments de
.
avec
un ensemble fini d'entiers de
strictement inférieurs à . Donner tous les éléments de
.


 mod .
mod .  1 mod .
1 mod .  1 mod
1 mod  1 mod .
1 mod . /
/ .
.  du système d'équations suivant
du système d'équations suivant  .
.
 du système d'équations suivant
du système d'équations suivant  .
.