Doc Théorème de Bolyai

Sommaire

Si deux figures sont obtenues en disposant les mêmes pièces d'un tangram, elles ont évidemment même aire. Le théorème de Bolyai affirme qu'il suffit que deux polygones aient même aire pour qu'il existe un jeu de pièces polygonales qui permette d'obtenir par recollement l'un ou l'autre des polygones. La démonstration de ce théorème est un peu longue mais assez élémentaire ; elle donne des méthodes de découpage. Dans les cas particuliers , on cherchera des solutions plus élégantes.

Equivalence par découpage et recollement

1. Définition
2. Propriétés
3. Transitivité

Théorème de Bolyai

• Enoncé
• Démonstration

Quelques exercices

---

Ce document accompagne une partie du cours de géométrie de la licence scientifique générale (L3 pour des futurs professeurs des écoles à l'université Paris-Sud) . Il a pour but d'illustrer par des figures colorées et mobiles la notion d'équivalence par découpage et recollement et la démonstration du théorème de Bolyai. La démonstration est écrite en détail dans le livre de Daniel PERRIN, Mathématiques d'école, nombres, mesures et géométrie (Editions Cassini).
On consultera avec profit Aires et volumes : découpage et recollement (I), un article de Daniel Perrin en ligne sur Images des Mathématiques, CNRS.
Les figures mobiles utilisent Geogebra que vous devez autoriser à les afficher.

Quelques exercices

Dans chaque cas, on précisera comment le découpage est obtenu et on justifiera le recollement.

1. Proposer un découpage d'un carré permettant d'obtenir par recollement deux carrés de même aire.
2. Proposer un découpage d'un carré de côté $a$ permettant d'obtenir par recollement deux carrés de côtés $b$ et $c$.
3. Proposer un découpage d'un rectangle permettant d'obtenir par recollement un carré.
4. Proposer un découpage d'un carré permettant d'obtenir par recollement trois carrés de même aire.
5. Proposer un découpage de trois carrés de même aire permettant d'obtenir par recollement un carré.
6. Trois variantes d'un même problème :
   • Découper un carré pour obtenir par recollement 5 carrés de même aire.
   • Avec 5 carreaux de céramique identiques, carreler un grand carré.
   • Transformer une croix rouge en carré en deux coups de ciseaux.
7. Un calisson a la forme d'un losange formé de deux triangles équilatéraux dont on notera $a$ la longueur du côté. Ranger des calissons dans une boîte de la forme d'un calisson de côté $2a$ puis dans une boîte de forme hexagonale de côté $a$ puis de côté $2a$.
8. Problème du pâtissier .
9. Proposer un découpage d'un hexagone (resp. pentagone) en deux hexagones (resp. pentagones).
10. Proposer un découpage d'un triangle équilatéral (resp. hexagone régulier) en trois triangles équilatéraux (resp. hexagones réguliers).

Problème du pâtissier

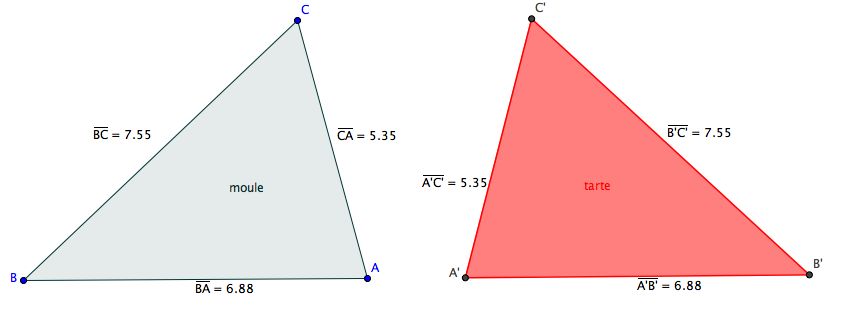
Comment mettre la tarte dans le moule ? On peut retourner la tarte dans le moule, les fruits au fond, ou découper la tarte et placer les morceaux fruits au-dessus dans le moule. Le pâtissier connaît le théorème de Bolyai donc il sait que la deuxième méthode est possible. Proposez une solution à quatre morceaux et une à trois seulement.

Découpage et recollement de polygones

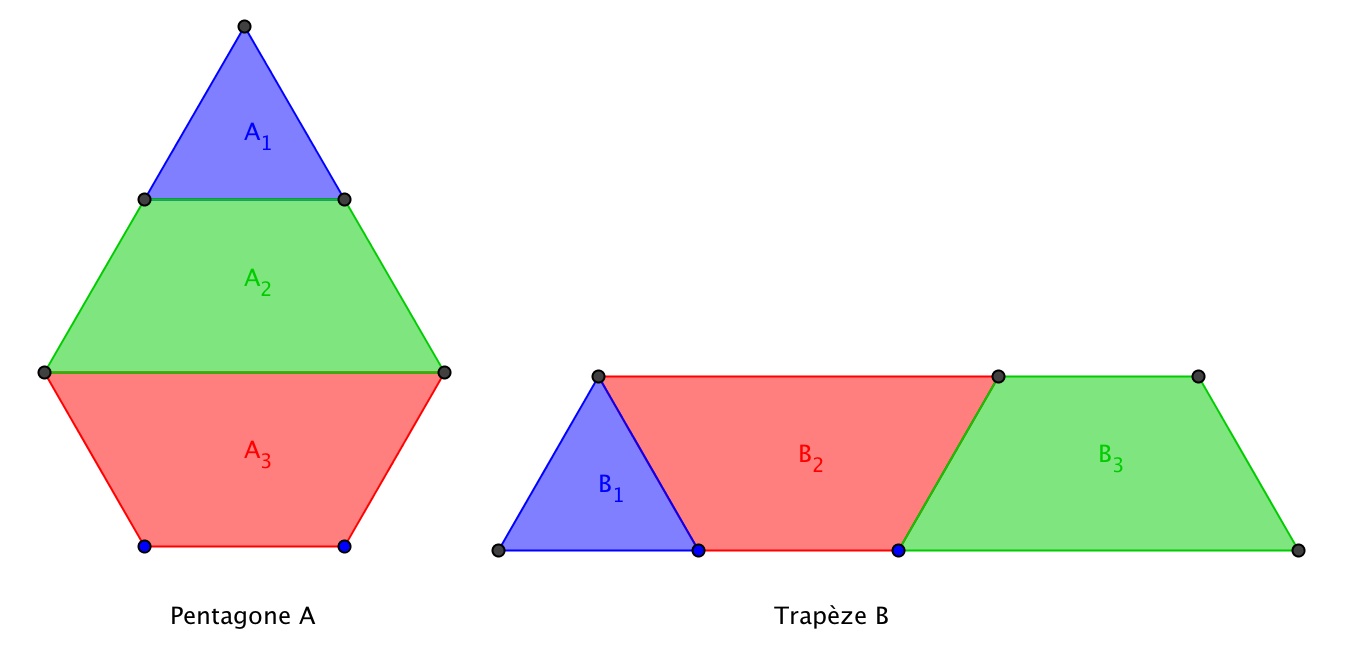
Exemple : Le pentagone est équivalent au trapèze.

Propriétés

(3) signifie que ~ vérifie trois propriétés :

1. la réflexivité : $A~A$
2. la symétrie : $A~B$ implique $B~A$
3. la transitivité explicitée ici est la clé de la démonstration du théorème de Bolyai.

Transitivité

Ici, on a trouvé un découpage du carré $A$ qui permet d'obtenir le rectangle $R_A$ par recollement et un découpage du triangle $B$ qui permet d'obtenir le rectangle $R_B$ par recollement. Comme $A$ et $B$ ont même aire les rectangles $R_A$et $R_B$, de largeur 1, ont même longueur, ils sont isométriques. En superposant le découpage rouge et le découpage bleu de $R$, on obtient un découpage vert de $R$ en morceaux plus nombreux qui permettent d'obtenir par recollement soit $A$, soit $B$.

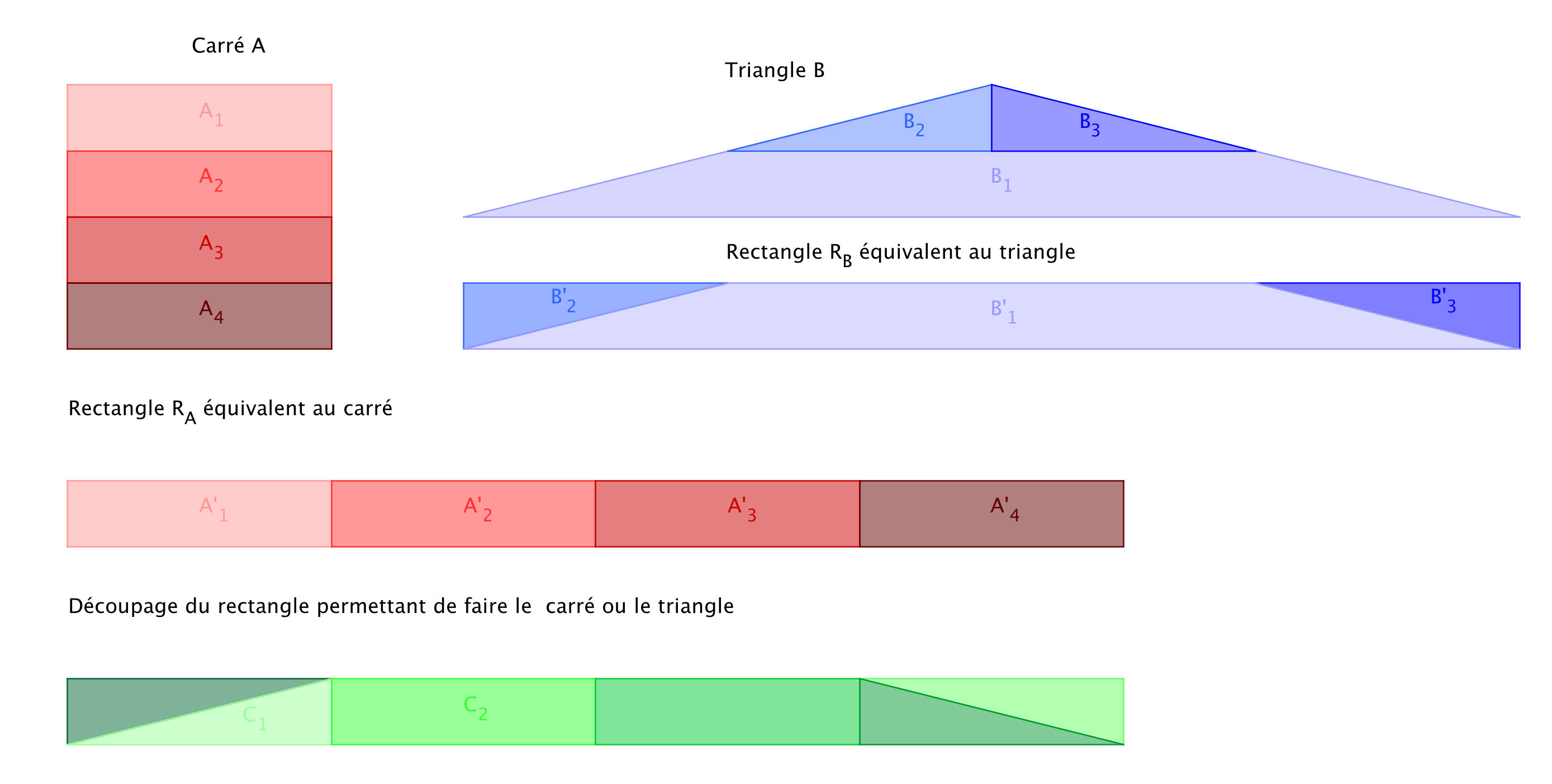
Théorème de Bolyai

La démonstration assez longue utilise sans cesse la transitivité de la relation ~ puisque par étape on passe d'un polygone $A$ à un rectangle $R$ équivalent à $A$ dont un côté a pour longueur l'unité. Les découpages utilisés sont exemplaires de la méthode mais dans les exercices on s'attachera à produire des découpages en peu de pièces.

Démonstration

Remarque: Ce résultat ne se généralise pas aux volumes. En général, deux polyèdres de même volume ne sont pas équivalents par découpage et recollement. Pour plus de détails, consulter Aires et volumes : découpage et recollement (II), un article de Daniel Perrin en ligne sur Images des Mathématiques, CNRS.

Démonstration

Etapes de la démonstration du Théorème de Bolyai :

1. Lemme fondamental
2. Du polygone au triangle
3. Du triangle au parallélogramme
4. Parallélogramme de côté particulier
5. Du parallèlogramme au rectangle

Lemme fondamental

Ce lemme implique le théorème de Bolyai en effet si $A$ et $B$ sont de même aire, ils seront équivalents par découpage et recollement l'un à $R_A$, l'autre à $R_B$. Or comme $R_A$ et $R_B$ ont un côté de longueur l'unité et sont de même aire, ils sont isométriques donc équivalents. Par transitivité $A$ et $B$ le seront aussi.

C'est le cas illustré dans la présentation de la transitivité de la relation ~ .

Du polygone au triangle

Si on peut trouver un découpage de n'importe quel triangle qui permette d'obtenir par recollement un rectangle dont un côté est de longueur 1, on pourra le faire pour tout polygone. En effet, on peut découper tout polygone en triangles. Il suffit donc de montrer le lemme fondamental pour les triangles.

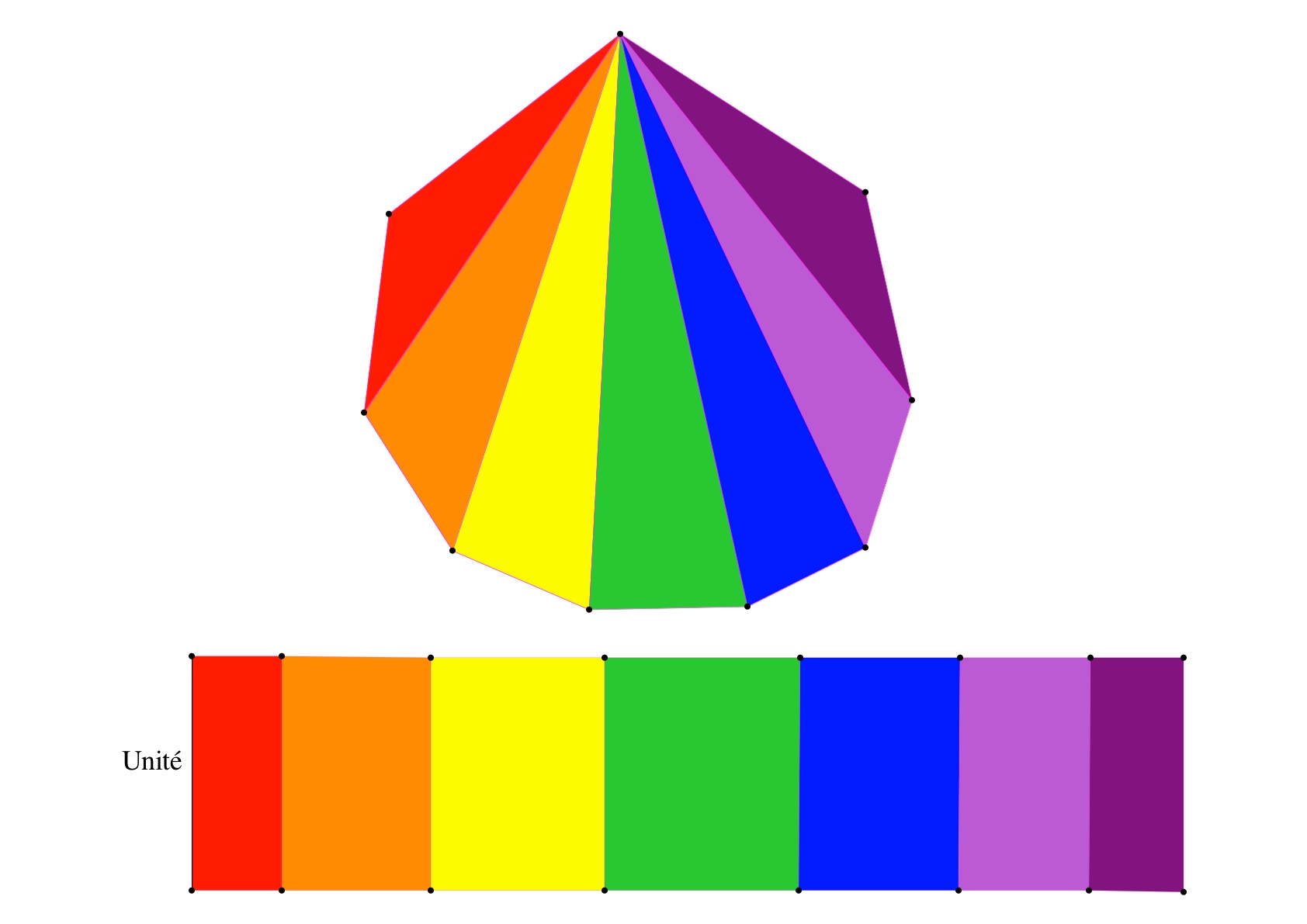
Du triangle au parallélogramme

On découpe le triangle $\mathrm{ABC}$ selon la droite des milieux $(\mathrm{MN})$ et on fait tourner le petit triangle rouge $\mathrm{AMN}$ autour du point $N$ en déplaçant le point $A\prime$. Le découpage de $\mathrm{ABC}$ en deux parties permet d'obtenir par recollement le parallélogramme $\mathrm{BMND}$.

Sur la figure, bouger le point $A$ change l'allure du triangle $\mathrm{ABC}$.

Du parallèlogramme au rectangle

Voici la dernière étape qui amène au rectangle de côté 1 annoncé dans le lemme fondamental.

Il est plus ou moins immédiat de découper $P$ pour obtenir un rectangle en gardant un côté de longueur $\mathrm{AB}$ : Figure dans le cas favorable et figure dans le cas défavorable .

cas favorable

Si le pied de la hauteur se trouve sur le côté $[\mathrm{AB}]$, il est simple de découper le parallélogramme pour obtenir un rectangle de côté l'unité.
En utilisant le point mobile $A\prime$, déplacez le triangle $A\prime H\prime D\prime$ pour transformer le parallélogramme en un rectangle.

cas défavorable

Si le pied de la hauteur du parallélogramme $\mathrm{ABCD}$ ne se trouve pas sur le côté $[\mathrm{AB}]$, on découpe, par des droites parallèles à $[\mathrm{AB}]$, le parallélogramme en tranches suffisamment petites afin de pouvoir transformer chaque petit parallélogramme en un rectangle comme dans le cas favorable . Faites-le en déplaçant les points $P$, $Q$, $R$ et $S$.
Il suffit ensuite d'empiler les rectangles obtenus en un rectangle de côté l'unité. Faites-le en déplaçant les points $T$, $U$, $V$ et $W$.