OEF champ curviligne
--- Introduction ---
Ce module regroupe pour l'instant 10
exercices sur les intégrales curvilignes de champs de vecteurs.
Cycles de Carnot
On appelle isothermes les courbes de niveau de la fonction
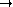
et adiabatiques les courbes de niveau de la fonction
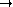 .
.
Intégrales curvilignes-1 3D
Soit
le champ défini sur
par
.
Calculer l'intégrale curviligne 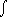 du champ
le long de la courbe
formée des segments qui joignent les points () à () et () à ().
du champ
le long de la courbe
formée des segments qui joignent les points () à () et () à ().
Intégrales curvilignes 1
Soit
le champ défini sur
par
.
Calculer l'intégrale curviligne 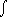
du champ
le long de la courbe
formée des segments qui joignent les points () à (), () à () et () à ().
Intégrales curvilignes-2 3D
Calculer l'intégrale curviligne de la forme différentielle
le long de
où
est la courbe (orientée) formée des segments qui joignent les points () à () et () à ( ).
Intégrales curvilignes 2
Calculer l'intégrale curviligne de la forme différentielle
le long de
où
est la courbe (orientée) formée des segments qui joignent les points () à (), () à ( ) et () à ().
Intégrales curvilignes 3
Calculer l'intégrale curviligne
où
est la courbe (orientée) formée des segments qui joignent les points () à (), () à ( ) et () à ().
Intégrale curviligne
Soit
une fonction de classe
sur
. L'intégrale curviligne de
le long de la courbe
d'équations paramétriques
, pour
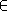 [ , ]
[ , ]
se ramène à une intégrale simple :
|
| |
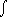 =
= 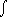 | |
(
,
,
)
1/2
|
|
| |
Remplissez les blancs.
Forme différentielle et champ 3D
Soit
= 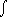
l'intégrale curviligne de la forme différentielle  =
=
le long d'une courbe
. Quel est le champ de
associé à  tel que
représente
?
tel que
représente
?
+
+
Forme différentielle et champ
Soit
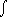
l'intégrale curviligne de la forme différentielle  =
=
le long d'une courbe
. Quel est le champ de
associé à  tel que
représente
tel que
représente
+
Travail 1
Calculer le travail effectué par le champ de forces
défini par
+
pour déplacer une particule le long d'un arc de cercle de rayon 1, de centre 0 et d'angle variant entre 0 et
dans le sens trigonométrique.
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les intégrales curvilignes. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, analysis, circulation,intégrale curviligne, courbe paramétrée,flux, masse
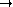
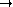
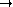 .
. 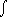 du champ
le long de la courbe
formée des segments qui joignent les points () à () et () à ().
du champ
le long de la courbe
formée des segments qui joignent les points () à () et () à ().
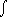
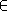 [ , ]
[ , ]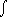 =
= 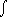
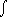
 =
=
 tel que
représente
?
tel que
représente
? 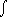
 =
=
 tel que
représente
tel que
représente