OEF min-max2
--- Introduction ---
Ce module regroupe pour l'instant 12 exercices sur les extrema des fonctions de deux variables.
Distance d'un point à une conique
Quelle est la distance de la courbe d'équation
à l'origine ?
xrange -, + yrange -, + parallel -,0,+,0,0,1,40,grey parallel -,0,+,0,0,-1,40,grey parallel 0,-,0,+,1,0,40,grey parallel 0,-,0,+,-1,0,40,grey arrow 0,0, 0,1,10,black arrow 0,0, 1, 0 ,10,black vline 0,0, black hline 0,0, black levelcurve darkred, , levelcurve green,
Commencer par répondre aux questions suivantes:
On interprète ce problème comme un problème d'extrema liés. Il s'agit donc trouver le minimum de la fonction de deux variables
définie par
soumise à la contrainte
Avec
et
, on a grad
(
,
)
grad
(
,
)
Ces deux vecteurs sont liés au point
si leur déterminant
est égal à
.
Rappelons que grad
et grad
sont liés si
Donner la valeur du point critique
pour laquelle
est minimum sur la courbe
. A=(
,
)
La distance minimale de la courbe au point
est donc égale à
L'exercice a plusieurs étapes
Distance d'un point à une courbe*
Quelle est la distance de la courbe d'équation
à l'origine ?
xrange -, + yrange -, + parallel -,0,+,0,0,1,40,grey parallel -,0,+,0,0,-1,40,grey parallel 0,-,0,+,1,0,40,grey parallel 0,-,0,+,-1,0,40,grey arrow 0,0, 0,1,10,black arrow 0,0, 1, 0 ,10,black vline 0,0, black hline 0,0, black levelcurve darkred, , levelcurve green,
Commencer par répondre aux questions suivantes :
On interprète ce problème comme un problème de maxima liés. Il s'agit donc trouver le maximum de la fonction de deux variables
définie par
soumise à la contrainte
Avec
et
, on a grad
(
,
)
grad
(
,
)
Ces deux vecteurs sont liés au point
si leur déterminant
est égal à
.
Ainsi, grad
et grad
sont liés si
Donner la valeur d'un point critique
pour laquelle
est minimum sur la courbe
,
) La distance minimale de la courbe au point
est donc égale à
Fonction affine sur une ellipse
Calculer le point où est atteint le de la fonction
définie par
soumis aux contraintes
et
.
Extremum I
Soit
une fonction de deux variables de
dans  de classe
et
un point de
. On suppose que :
de classe
et
un point de
. On suppose que :
,
,
,
,
.
Le point
est-il un point critique?
Le point
est un
Extremum II
Soit
la fonction de
dans  définie par
définie par
.
Le point
est un :
Point critique et courbes de niveau
Soit
une fonction de deux variables de
dans  de classe
et
un point de
. On suppose qu'au voisinage de
, on a :
de classe
et
un point de
. On suppose qu'au voisinage de
, on a :

où la fonction  tend vers 0 lorsque
tend vers
. Parmi les trois dessins suivants, lequel peut représenter les lignes de niveau de
au voisinage de
?
tend vers 0 lorsque
tend vers
. Parmi les trois dessins suivants, lequel peut représenter les lignes de niveau de
au voisinage de
?
Maximum (avec bord, canalisation)
On construit une canalisation de forme trapézoidale avec une plaque de largeur . Quelles sont les valeurs optimales de la longueur du côté incliné et de l'angle qu'il fait avec la verticale pour que le flux passant dans la gouttière soit maximal ?
xrange -3.5, 3.5 yrange -3.5, 3.5 linewidth 3 arc 3.3, 3,3, 240,300, black lines green ,-3,1,-2,-1, 2,-1,3,1 line -3,1,3,1, red fill 0,0, skyblue transparent red
xrange -4.5, 4.5 yrange -4.5, 4.5 line -2,-1,-2,1,black text black,-3,1, medium, y text black,-3.5,0, medium, x arc -2,-1,2,2, 90,130, black linewidth 3 lines green ,-4,1,-2,-1, 2,-1,4,1
Commencer par répondre aux questions suivantes: On note
la longueur du côté incliné et
l'angle comme sur le dessin.
La surface à rendre maximum est donnée par la fonction
donnée par
sur le domaine
défini par
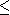 x
x 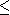
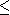 y
y 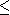
Calculer le point critique de
qui se trouve à l'intérieur du domaine
,
) et la valeur de la fonction
en ce point :
Pour information, voici les lignes de niveau de
xrange -0.5, yrange -0.5, parallel -1,0,,0,0,1,40,grey parallel -1,0,,0,0,-1,40,grey parallel 0,-1,0,,1,0,40,grey parallel 0,-1,0,,-1,0,40,grey levelcurve darkred, , vline 0,0, black hline 0,0, black linewidth 3 lines green, 0,0,0,pi/2, /2,pi/2, /2,0,0,0 linewidth 1 arrow 0,0, 0,1,10,black arrow 0,0, 1, 0 ,10,black disk ,, 5,blue
Quel est le maximum de
sur le bord de
Conclure : Le petit côté vaut
et l'angle (en radians) est
L'exercice a plusieurs étapes
Extremum sur un domaine à bord
Trouver le global de la fonction
définie par
sur la région triangulaire fermée
de sommets
,
et
en répondant d'abord aux questions suivantes :
Combien de points critiques y-a-t-il à l'intérieur de
?
- Donner les coordonnées de ce point critique
- Calculer la valeur de la fonction
en ce point :
- Pouvez-vous conclure sans autre calcul ?
On a
.
- Quelle est la valeur du de la fonction sur le bord
?
- Quel est la valeur du de la fonction sur le bord
?
- Quelle est la valeur du de la fonction sur le bord
?
- Quel est le de la fonction sur
xrange , yrange , fpoly grey,,, text black, , medium, A text black, , medium,B text black, , medium,C
L'exercice a plusieurs étapes
Maximum d'un volume avec conditions I
Calculer le volume du plus grand parallélépipède rectangle - ayant
comme sommet,
- dont les arêtes sont parallèles aux axes de coordonnées,
- qui se trouve dans le premier octant (coordonnées positives ou nulles),
- dont le sommet opposé à
est dans le plan d'équation
en répondant d'abord aux questions suivantes :
Calculer le volume comme une fonction
de
.
Le domaine de définition
de la fonction
donnée par
correspondant au problème posé est un triangle :
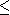
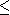 ,
,
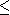
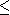
Quelles hypothèses doit-on utiliser pour en déduire que
admet un maximum sur
défini par les inégalités
(mettez-en le moins possible même si certaines des conditions sont réalisées) : - Se sert-on directement de l'hypothèse que
- Se sert-on directement de l'hypothèse que
- Se sert-on directement de l'hypothèse que
- Se sert-on directement de l'hypothèse que
- Se sert-on directement de l'hypothèse que
- Se sert-on directement de l'hypothèse que
Combien de points critiques la fonction
donnée par
a-t-elle à l'intérieur de
Le point critique de
à l'intérieur de
est (
,
).
La fonction
est nulle sur les bords de
. Comme la fonction
admet un maximum, qu'elle est à valeurs positives et qu'elle est nulle sur le bord, le point critique
est nécessairement un maximum Calculer les longueurs
,
et
des trois côtés correspondant à la boîte de volume maximal et ce volume .
L'exercice a plusieurs étapes
Maximum d'un volume avec conditions II
Quel est le volume maximum d'une boîte rectangulaire sans couvercle fabriquée avec
de carton ? Commencer par répondre aux questions suivantes
On interprète ce problème comme un problème de maxima liés.
Il s'agit donc trouver le maximum de la fonction de trois variables
définie par
soumise à la contrainte
Avec
et
on a grad
(
,
,
)
grad
(
,
,
)
Ces deux vecteurs sont liés au point
si leur produit vectoriel (
,
,
)
est égal à
.
La valeur de
(donnant le volume) pour un point dont une des coordonnées est nulle est égale à
. un tel point
un maximum.
Ainsi, grad
et grad
sont liés si
Il y a un seul point critique pour ce problème dont toutes les coordonnées sont non nulles, il s'agit du point
(
,
,
)
et le volume correspondant vaut
L'exercice a plusieurs étapes
Méthode des moindres carrés
On a quelques raisons de croire que deux grandeurs
et
sont reliées par une relation affine
. Les données expérimentales donnent les points
suivants : Chercher l'équation de la droite par la méthode des moindres carrés : on minimise la somme des carrés des déviations
y=
x +
xrange -1,+1 yrange -1,+1 hline black, 0,0 vline black, 0,0 arrow 0,0,0,1,10,black arrow 0,0,1,0,10,black plot red , ()*x+()
Distance aux tangentes d'une conique
Calculer le point de la conique 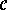 d'équation
dont la tangente à
d'équation
dont la tangente à 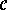 est à la plus grande distance du point
.
The most recent version
est à la plus grande distance du point
.
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les extrema des fonctions de deux variables. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, analysis, maximum, minimum, extremum, point critique, maxima, minima

 de classe
et
un point de
. On suppose que :
de classe
et
un point de
. On suppose que :  définie par
définie par  de classe
et
un point de
. On suppose qu'au voisinage de
, on a :
de classe
et
un point de
. On suppose qu'au voisinage de
, on a : 
 tend vers 0 lorsque
tend vers
. Parmi les trois dessins suivants, lequel peut représenter les lignes de niveau de
au voisinage de
?
tend vers 0 lorsque
tend vers
. Parmi les trois dessins suivants, lequel peut représenter les lignes de niveau de
au voisinage de
? 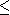 x
x 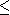
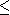 y
y 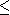
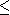
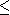 ,
,
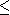
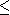
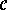 d'équation
dont la tangente à
d'équation
dont la tangente à 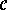 est à la plus grande distance du point
.
The most recent version
est à la plus grande distance du point
.
The most recent version