Géométrie du plan : Frises et Pavages
Géométrie du plan : Frises et Pavages
La première partie de ce document est conçue comme une initiation à la géométrie du plan et une introduction à l'utilisation des groupes. Ce travail mène naturellement à l'étude des frises (ou ornement linéaires) et des pavages, ce que nous faisons ici.
Il a été développé au fil d'un cours d'ouverture à l'intention d'étudiants de L1 et L2 comme une promenade dans la géométrie du plan. Il doit beaucoup à des documents que m'a donnés Daniel Perrin lors de la préparation de ce cours.

Le plan affine est noté .
I Frises
Géométrie du plan : Frises et Pavages
→ I Frises

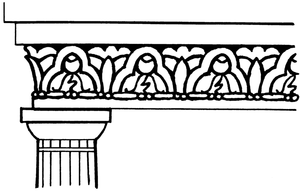
Pour analyser une frise, il faut
- déterminer la bande , c'est-à-dire la direction des translations et un motif de translation ;
- trouver son groupe ponctuel , les directions des axes de réflexion, l'ordre des rotations ;
- placer les éléments de symétrie (centres de rotation, axes de réflexion, axes de réflexion glissée).
- déterminer le groupe de ses isométries parmi une liste finie que nous allons donner.
- déterminer un motif de base .
Faisons d'abord l'étude mathématique.
I-2 Groupe discret, groupe ponctuel
Géométrie du plan : Frises et Pavages
→ I Frises
I-1 Ornement linéaire
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-1 Ornement linéaire
Prenons une bande
, c'est-à-dire la zone du plan comprise
entre deux droites parallèles et un dessin dans cette bande, c'est-à-dire
un sous-ensemble de la bande ou un dessin coloré (un nombre fini de sous-ensembles
disjoints de cette bande) contenu dans un parallélogramme et translatons-le
dans la direction de la bande de manière à ce qu'il n'y ait pas de superposition, on obtient
une frise.
Définition
Un ornement linéaire ou frise est
un dessin
de
dont le groupe des translations
de
est de la forme
où
est
un vecteur non nul.
Définition
Un motif de translation
est une partie fermée de
, connexe (c'est-à-dire d'un seul
morceau) telle que les translatés de
par les translations de
recouvrent
:
et telle que l'intersection de deux tels translatés soit contenue dans leur
frontière.
Un motif de base
est une partie fermée de
, connexe, telle que les images de
par les isométries de
recouvrent
:
et telle que l'intersection de deux tels transformés soit contenue dans leur
frontière.
Par exemple, un parallélogramme de longueur (dans la direction de la bande) la norme de
est un motif de translation. Par contre, le motif de base dépend de la structure du groupe des
isométries.
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-1 Ornement linéaire
I-2 Groupe discret, groupe ponctuel
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-2 Groupe discret, groupe ponctuel
Définition
Un groupe de symétrie d'un ensemble
est discret
s'il existe des réels strictement positifs
et
tel que
- pour toute translation de vecteur non nul appartenant à , ;
-
pour toute rotation d'angle
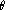 appartenant à
,
.
appartenant à
,
.
Proposition
Si
est discret et laisse fixe un point
, il est fini.
Proposition
Le groupe d'un ornement linéaire est discret.
Proposition
Soit
un point de
.
Le groupe ponctuel
d'un ornement linéaire est fini.
Désormais, est un ornement linéaire dont le groupe des translations de est de la forme avec un vecteur non nul. On fixe une origne du plan.
Proposition
Soit
la droite vectorielle de direction
et
la perpendiculaire à
passant par
.
Tout élément de
est de la forme
où
est une translation et
Autrement dit, le groupe ponctuel
de
est contenu dans le groupe
.Démonstration
Soit
et écrivons
avec
une isométrie
fixant l'origne et
un vecteur.
L'isométrie transformée de par est égale à . Comme appartient à , aussi ; donc . Comme et ont même norme, est ou .
La droite vectorielle de direction est donc stable par ; il en est de même de sa perpendiculaire ( conserve des angles). Donc, peut être : l'identité, la symétrie centrale par rapport à , la réflexion axiale par rapport à ou la réflexion axiale par rapport à .
L'isométrie transformée de par est égale à . Comme appartient à , aussi ; donc . Comme et ont même norme, est ou .
La droite vectorielle de direction est donc stable par ; il en est de même de sa perpendiculaire ( conserve des angles). Donc, peut être : l'identité, la symétrie centrale par rapport à , la réflexion axiale par rapport à ou la réflexion axiale par rapport à .
Fin de la démonstration
Les sous-groupes de sont faciles à décrire. Il y en a cinq ;
-
;
-
;
-
;
-
;
-
.
Exercice
Quel est le groupe ponctuel de chacune des frises suivantes :
Voir aussi Groupe ponctuel d'une frise
Voir aussi Groupe ponctuel d'une frise
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-2 Groupe discret, groupe ponctuel
I-3 Droite affine invariante de la bande
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-3 Droite affine invariante de la bande
Proposition
Il existe au moins une droite affine
parallèle à
invariante par
.
Démonstration
Les droites invariantes par le groupe des translations
de
sont les droites de direction
. Nous allons donc chercher la droite
parmi
ces droites. Elle doit être invariante par les isométries de
qui ne
sont pas des translations.
Prenons une isométrie de qui n'est pas une translation. Elle s'écrit
avec
,
,
avec
de direction
et
perpendiculaire à
.
Faisons quelques remarques sur les isométries que l'on peut obtenir
et les droites qu'elles laissent invariantes :
Reprenons maintenant les cinq cas de groupes ponctuels possibles.
Prenons une isométrie de qui n'est pas une translation. Elle s'écrit
- : est une symétrie centrale de centre un point ; toute droite passant par et de direction est invariante par ;
-
avec
droite
de direction
et
parallèle à
(réflexion ou symétrie glissée) ;
on a alors
. Donc
est un multiple de
.
La droite
est stable par
.
-
avec
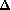 droite
de direction
et
parallèle à
droite
de direction
et
parallèle à
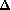 ;
on a alors
. Donc
appartient à
; comme il
est perpendiculaire à
, il est nul. Autrement dit,
est une réflexion d'axe
;
on a alors
. Donc
appartient à
; comme il
est perpendiculaire à
, il est nul. Autrement dit,
est une réflexion d'axe
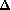 perpendiculaire à
.
Toute droite de direction
est stable par
.
perpendiculaire à
.
Toute droite de direction
est stable par
.
Reprenons maintenant les cinq cas de groupes ponctuels possibles.
-
: toute droite de direction
est invariante par
.
-
;
est engendré par
et par
pour
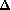 une droite de direction
; toute droite de direction
est invariante par
.
une droite de direction
; toute droite de direction
est invariante par
.
-
; toute droite de direction
est invariante par
.
-
; il y a dans
une réflexion
ou une symétrie glissée
d'axe une droite
de direction
. Cette droite est invariante par les
translations de
et par
donc par
.
-
;
est engendré par
et par
,
et
avec
parallèle à
,
une droite de direction
,
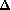 perpendiculaire à
et
un point. Montrons que la droite
est stable par
:
il reste à montrer que
est stable par
(pour les autres, on
utilise les cas précédents). Pour cela, il suffit de montrer que
appartient
à
. L'isométrie suivante appartient à
:
avec parallèle à
perpendiculaire à
et
un point. Montrons que la droite
est stable par
:
il reste à montrer que
est stable par
(pour les autres, on
utilise les cas précédents). Pour cela, il suffit de montrer que
appartient
à
. L'isométrie suivante appartient à
:
avec parallèle à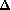 .
Son carré est égal à
et
. Donc
et
.
.
Son carré est égal à
et
. Donc
et
.
Fin de la démonstration
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-3 Droite affine invariante de la bande
I-4 Classification
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-4 Classification
Théorème
Il y a exactement 7 groupes de symétrie d'ornements à conjugaison près
par une similitude.
On choisit une droite
invariante par
parallèle à
.Exercice
A partir des lettres de l'alphabet, dessiner
un ornement de chaque type.
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-4 Classification
I-5 Nomenclature
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-5 Nomenclature
Expliquons les principes de la nomenclature pour les frises
(il y a diverses nomenclatures, le tout est d'en choisir une et
de la comprendre, elles fonctionnent toutes sur le même principe !)
On fait aussi le cas des pavages (le groupe des translations est engendré
par deux translations de vecteurs non colinéaires).
On choisit les axes de manière à ce que les axes de symétrie soient perpendiculaires à l'un ou l'autre. Il y a plusieurs caractères. Leur signification est :
A partir de ces règles, on peut simplifier en supprimant ce qui n'est pas essentiel, c'est-à-dire n'apportera pas de confusion possible ... On enlève par exemple le 1 en deuxième position, le en dernière position (puisqu'il indique qu'il n'y a rien) ... On remplace aussi de temps en temps le par un ...
On choisit les axes de manière à ce que les axes de symétrie soient perpendiculaires à l'un ou l'autre. Il y a plusieurs caractères. Leur signification est :
- une lettre
(en dimension 1) ,
,
(en dimension 2) :
- quand les translations sont dans une seule direction (groupe de translation isomorphe à );
- si les centres de rotation se trouvent sur les axes de symétrie;
- si les centres de rotation ne se trouvent pas sur les axes de symétrie.
- un entier indiquant le plus grand ordre de rotation
- un symbole indiquant un axe de symétrie perpendiculaire à l'axe
des
- pour symétrie m iroir,
- pour symétrie g lissée
- pour rien
- (cas des pavages) un symbole indiquant un axe de symétrie faisant un angle
 (différent de l'angle droit) avec l'axe des
.
(différent de l'angle droit) avec l'axe des
.
- pour symétrie m iroir,
- pour symétrie g lissée
- pour rien
A partir de ces règles, on peut simplifier en supprimant ce qui n'est pas essentiel, c'est-à-dire n'apportera pas de confusion possible ... On enlève par exemple le 1 en deuxième position, le en dernière position (puisqu'il indique qu'il n'y a rien) ... On remplace aussi de temps en temps le par un ...
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-5 Nomenclature
II Réseaux et pavages
Géométrie du plan : Frises et Pavages
→ II Réseaux et pavages



Nous allons étudier ici les pavages réguliers. On parle alors simplement de pavé au lieu de pavé fondamental. Nous reviendrons plus tard sur ce que signifie les classifier.
Dans le paragraphe suivant, nous allons étudier le cas particulier où le pavé fondamental est un parallélogramme, c'est-à-dire nous intéresser d'abord au sous-groupe des translations.
Passons à un pavage . Soit le sous-groupe des translations et le réseau associé. Le groupe du pavage est contenu dans dans le groupe du réseau .
Géométrie du plan : Frises et Pavages
→ II Réseaux et pavages
II-1 Définition d'un pavage
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→ II-1 Définition d'un pavage
Définition
Des sous-ensembles de
(qu'on appelle alors pavés ) réalisent un
pavage de
si les conditions suivantes sont vérifiées :
- Chacun de ces sous-ensembles est un fermé borné (compact) d'intérieur non vide.
- La réunion de ces sous-ensembles est égale à .
- Deux quelconques de ces sous-ensembles ont toujours une intersection vide, ou une intersection contenue dans leur frontière.
Ne pas hésiter à donner aux mots frontière et intérieur leur sens en langage naturel.
Définition
Une autre définition directe possible est la suivante :Définition
On appelle pavage régulier du plan la donnée d'un compact
(appelé pavé fondamental )
de
,
d'intérieur non vide et d'un sous-groupe
du groupe des
isométries de
tel que
Le groupe des isométries du pavage est le groupe des isométries de laissant le pavage inchangé.
On utilisera aussi des pavage colorié : dans ce cas et sans donner de définitions précises et lourdes, les couleurs doivent être transformées par les isométries.
- si est d'intérieur non vide, .
Le groupe des isométries du pavage est le groupe des isométries de laissant le pavage inchangé.
On utilisera aussi des pavage colorié : dans ce cas et sans donner de définitions précises et lourdes, les couleurs doivent être transformées par les isométries.
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→ II-1 Définition d'un pavage
II-2 Réseaux
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→ II-2 Réseaux
II-2-2 Base réduite d'un réseau
Nous allons maintenant étudier les groupes de symétries d'un réseau et voir qu'il n'y a que 5 possibilités.
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→ II-2 Réseaux
II-2-1 Définition
Soient deux vecteurs
et
du plan affine
muni du repère affine
.
Dessinons l'ensemble des points
de
tels que
avec
et
entiers relatifs.
On appelle ces points des noeuds et leur ensemble un réseau .
Les vecteurs du réseau sont les vecteurs
.
On dit que
est une base du réseau.
Le pavé (maille du réseau) formé des points avec et compris entre 0 et 1 et le groupe de symétrie formé des translations avec et entiers relatifs forment un pavage du plan.
Le pavé (maille du réseau) formé des points avec et compris entre 0 et 1 et le groupe de symétrie formé des translations avec et entiers relatifs forment un pavage du plan.
Exercice
Dessiner les réseaux suivants et justifier leur
nom :
- : réseau oblique
- : réseau rectangle
- : réseau losange
- : réseau losange
- : réseau carré
- : réseau hexagonal ou équilatéral
II-2-2 Base réduite d'un réseau
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-2 Réseaux
→ II-2-2 Base réduite d'un réseau
Un réseau a de nombreuses bases. On aimerait trouver des bases qui soient le
plus orthonormées possibles : norme des vecteurs petite et angle des vecteurs le plus
proche possible de
.
Démonstration
Pour construire une base réduite, quelques idées à comprendre d'abord :
Exercice [ Retrancher à un multiple de ]
Exercice [ Comment choisir ce multiple ]
Démonstration
Proposition
Soit
un réseau. On peut trouver une base
de
telle que
- .
- .
Proposition
Soit
un réseau et
une base réduite.
Alors,
est de norme minimale parmi les vecteurs de
et
est de norme minimale parmi les vecteurs de
différents
de
.
Démonstration
Soit
une base réduite. Posons
Si
est un vecteur de
et
,
-
:
Si
ou
est nul, cela est clair. Sinon, on développe :
De plus, on a l'égalité si et seulement si , et , autrement dit pour les vecteurs dans le cas où l'angle de et de est de 60 degrés.
- si
,
:
Si
, cela est clair. Sinon,
De plus, on a l'égalité si et seulement si , et , autrement dit pour les vecteurs dans le cas où l'angle de et de est de 60 degrés. Sans oublier bien sûr les vecteurs et éventuellement .
Fin de la démonstration
Pour construire une base réduite, quelques idées à comprendre d'abord :
Exercice [ Retrancher à un multiple de ]
Vérifier que si deux vecteurs
et
font un angle
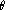 compris entre 0 et
, alors
est de norme plus petite que
et l'angle entre
et
est plus grand que l'angle
compris entre 0 et
, alors
est de norme plus petite que
et l'angle entre
et
est plus grand que l'angle
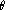 .
.
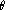 compris entre 0 et
, alors
est de norme plus petite que
et l'angle entre
et
est plus grand que l'angle
compris entre 0 et
, alors
est de norme plus petite que
et l'angle entre
et
est plus grand que l'angle
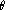 .
. Exercice [ Comment choisir ce multiple ]
Comment trouver
entier pour que
soit de norme minimale
parmi les vecteurs de la forme
pour
entier ?
Étudier la fonction
définie par
.
Que peut-on dire alors de l'angle de
avec
,
c'est-à-dire du produit scalaire
?
Algorithme
On part des deux vecteurs de base du réseau et on
appelle
celui qui est de plus petite norme et
l'autre.
Soit
l'entier le plus proche de
.
Ainsi,
et
-
Si la norme de
est plus petite que celle de
,
on remplace
par
et
par
.
- Si le produit scalaire de et de (les nouveaux) est négatif, on remplace par .
- On recommence.
- Sinon (
), on choisit
ou
,
de manière à ce que
;
alors,
est une base réduite car
Proposition
- si , les seuls vecteurs de norme sont et ainsi que si l'angle de et de est .
- si , les seuls vecteurs de norme sont . Les seuls vecteurs de norme sont .
Démonstration
Supposons
et soit
.
Les vecteurs
et
conviennent bien sûr.
Pour
et
différents de 0, on a
Pour avoir l'égalité, il faut que
et que
,
.
On obtient alors les vecteurs
.
Supposons maintenant . On a déjà vu que les seuls vecteurs de norme sont .
Supposons maintenant . On a déjà vu que les seuls vecteurs de norme sont .
Fin de la démonstration
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-2 Réseaux
→ II-2-2 Base réduite d'un réseau
II-2-3 Condition cristallographique
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-2 Réseaux
→ II-2-3 Condition cristallographique
Proposition
Soit
un réseau.
- Toute rotation du groupe de symétrie d'un réseau est d'ordre 1, 2, 3, 4 ou 6.
- Soit un sous-groupe fini du groupe de symétrie de . Alors, est un des groupes , pour , 2, 3, 4 ou 6.
Ainsi, les ordres possibles de sont 1, 2, 3, 4, 6, 8 ou 12.
Nous utiliserons dans la démonstration le principe de conjugaison : L'image du centre de rotation d'une rotation d'un groupe de symétrie par une autre rotation du groupe de symétrie est encore un centre de rotation d'un élément du groupe.
Démonstration
Soit
le groupe de symétrie d'un réseau.
Soient deux rotations
et
appartenant à
de centre respectivement
et
et d'ordre
. Prenons-les de manière
que la distance de
à
soit minimale [demande un mot d'explication].
Soit
l'ordre de
. L'isométrie
est une rotation de centre
.
L'angle
est égal à
et le triangle est isocèle en
.
On a donc
. Comme
est supérieur ou égal
à
, on a
, donc
et
.
Donc est égal à 1, 2, 3, 4, 5 ou 6. Éliminons le cas .
Supposons qu'il y ait une rotation d'ordre 5 et prenons deux centres et d'ordre 5 à distance minimum. Si on transforme le centre de rotation par la rotation de centre et ses puissances, on obtient cinq points sur le cercle de centre et de rayon . On recommence en transformant les centres de rotation par les rotations de centre . Un petit calcul (ou un dessin) montre que l'on peut alors trouver deux centres de rotation plus proches que ne le sont et , contradiction.
Donc est égal à 1, 2, 3, 4, 5 ou 6. Éliminons le cas .
Supposons qu'il y ait une rotation d'ordre 5 et prenons deux centres et d'ordre 5 à distance minimum. Si on transforme le centre de rotation par la rotation de centre et ses puissances, on obtient cinq points sur le cercle de centre et de rayon . On recommence en transformant les centres de rotation par les rotations de centre . Un petit calcul (ou un dessin) montre que l'on peut alors trouver deux centres de rotation plus proches que ne le sont et , contradiction.
Fin de la démonstration
Remarque
Les cas
, 3, 4, 6 ne peuvent pas être éliminés par cet argument :
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-2 Réseaux
→ II-2-3 Condition cristallographique
II-2-4 Les types de réseaux
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-2 Réseaux
→ II-2-4 Les types de réseaux
Soit (
,
) une base réduite. Notons
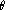 l'angle de
et
de
. Il est compris entre
et
(entre 60 et 90 degrés).
l'angle de
et
de
. Il est compris entre
et
(entre 60 et 90 degrés).
Dans chacun de ces cas, calculons le groupe des isométries de laissant fixe l'origine. On note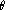 l'angle des vecteurs
et
pour
une base réduite.
l'angle des vecteurs
et
pour
une base réduite.
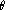 l'angle de
et
de
. Il est compris entre
et
(entre 60 et 90 degrés).
l'angle de
et
de
. Il est compris entre
et
(entre 60 et 90 degrés).- réseau oblique : aucune relation spéciale entre les vecteurs
- réseau rectangle : et sont perpendiculaires ;
- réseau losange : et sont de même longueur ;
- réseau carré : et sont perpendiculaires et de même longueur ;
- réseau hexagonal ou équilatéral : et sont de même longueur et forment un angle de 60 degrés ;
Dans chacun de ces cas, calculons le groupe des isométries de laissant fixe l'origine. On note
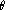 l'angle des vecteurs
et
pour
une base réduite.
l'angle des vecteurs
et
pour
une base réduite.
Proposition
Le groupe
est déterminé de la manière suivante :
- réseau oblique, p1
-
réseau rectangle, p1mm
, . Le groupe est le groupe d'un rectangle, il est diédral d'ordre 4 ( , mais on le connait aussi sous le nom de groupe de Klein ) :
Exemple- réseau losange, p6mm
- réseau carré, p4mm
- réseau hexagonal ou équilatéral, c1mm
DémonstrationRappelons, que et ont été choisis de manière à ce que et que .
Le groupe ccontient toujours l'identité et la symétrie centrale de centre .
Soit une isométrie laissant fixe .- Supposons d'abord que
. Les seuls vecteurs de norme
sont
. Donc,
.
On pose
ou
, de manière à ce que
.
Que peut-on dire de
?
Lorsque est différent de , les seuls vecteurs de norme égale à celle de sont , donc . On a d'autre part .- Si , on a nécessairement . Donc est l'identité et est soit ou l'identité.
- Si
, on peut avoir
ou
.
Donc
est égale à
ou
et
est égale à
,
,
ou à
.
- Si
est égal à
, on peut aussi avoir
puisque
et est alors égale à la réflexion par rapport à la droite vectorielle de direction . Finalement, peut être égale à , , ou à . Dans ce cas, le parallélogramme construit à l'aide des vecteurs , (qui forment une autre base de ) est un losange. Le parallèlogramme construit à partir de la base réduite n'est ni un rectangle, ni un losange ...
- Supposons maintenant que
.
- Lorsque est différent de , ce qui signifie ici que l'angle de et est différent de 60 degrés ( ), les quatre vecteurs , , , sont de même norme. En utilisant la condition de conservation du produit scalaire, on vérifie qu'on peut obtenir , ou , , c'est-à-dire , , , , , .
- Lorsque est égal à , c'est-à-dire lorsque l'angle de et est égal à 60 degrés, les six vecteurs , , , , et sont de même norme que . Si , . On essaye les cinq possibilités restantes pour ; seules sont possibles (déjà trouvée) ou , ce qui donne la rotation d'angle . On fait de même pour et on trouve sans étonnement les rotations d'angle avec .
Fin de la démonstration
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-2 Réseaux
→ II-2-4 Les types de réseaux
II-2-5 Que signifie classifier ?
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-2 Réseaux
→ II-2-5 Que signifie classifier ?
Nous venons de calculer le groupe des isométries
laissant fixe un réseau
et l'origine
.
On a obtenu quatre groupes possibles non isomorphes :
,
,
et
. On a d'autre part obtenu deux fois le groupe
.
Comment peut-on les distinguer ?
On a plusieurs manières de dire que deux réseaux sont équivalents
mais ces manières ne sont pas équivalentes.
Les notations sont perso ...
Pas très intéressant : deux réseaux sont toujours (lin)-équivalents.
Très restrictif : en "déplaçant" le réseau dans le plan euclidien (en le translatant, en le faisant tourner, en zoomant, en le reflétant dans un miroir ...), on obtient un réseau équivalent et simplement comme cela.
Un peu mieux : il y a maintenant quatre types de réseaux à "groupe-équivalence près" correspondant aux groupes , , et .
Cette définition permet de retrouver les cinq types de réseaux oblique, rectangle, carré, losange et hexagonal. Si vous disposez de deux réseaux de même type, pour montrer qu'ils sont (lin-groupe)-équivalents, on choisit pour une application linéaire envoyant une base réduite de l'un sur une base réduite de l'autre. Mais il reste quelque chose à montrer : le réseau losange et le réseau rectangle ne sont pas équivalents, c'est-à-dire qu'il n'existe pas d'application linéaire telle et telle que
Démonstration
Soit le groupe des translations de , c'est-à-dire le groupe des pour .
Les définitions précédentes sont encore valables en remplaçant par et donnent le même résultat. Cela vient de la proposition suivante :
Démonstration
Cette proposition peut sembler évidente. Cependant, le fait que est un réseau joue un rôle important. Cela ne serait pas vrai pour n'importe quel ensemble à la place de .
Les notations sont perso ...
Définition
Deux réseaux
et
sont (lin)-équivalents
s'il existe une application linéaire
de
dans
tels que
.
Pas très intéressant : deux réseaux sont toujours (lin)-équivalents.
Définition
Deux réseaux
et
sont (sim)-équivalents (semblables)
s'il existe une similitude
de
dans
tels que
.
Très restrictif : en "déplaçant" le réseau dans le plan euclidien (en le translatant, en le faisant tourner, en zoomant, en le reflétant dans un miroir ...), on obtient un réseau équivalent et simplement comme cela.
Définition
Deux réseaux
et
sont (groupe)-équivalents si leurs groupes
d'isométries linéaires
et
sont isomorphes.
Un peu mieux : il y a maintenant quatre types de réseaux à "groupe-équivalence près" correspondant aux groupes , , et .
Définition
Deux réseaux
et
sont (lin-groupe)-équivalents s'il existe
une application linéaire
de
dans
telle que
et telle que
Cette définition permet de retrouver les cinq types de réseaux oblique, rectangle, carré, losange et hexagonal. Si vous disposez de deux réseaux de même type, pour montrer qu'ils sont (lin-groupe)-équivalents, on choisit pour une application linéaire envoyant une base réduite de l'un sur une base réduite de l'autre. Mais il reste quelque chose à montrer : le réseau losange et le réseau rectangle ne sont pas équivalents, c'est-à-dire qu'il n'existe pas d'application linéaire telle et telle que
Démonstration
Soit
une réflexion de
, la droite invariante est de direction un
des vecteurs du réseau
. Si
existait, alors
serait une
réflexion par rapport à une droite de direction un des vecteurs du réseau
.
Mais une telle réflexion n'existe pas dans
.
Fin de la démonstration
Soit le groupe des translations de , c'est-à-dire le groupe des pour .
Les définitions précédentes sont encore valables en remplaçant par et donnent le même résultat. Cela vient de la proposition suivante :
Proposition
Soit
. Alors,
avec
et
. Autrement dit, le groupe
ponctuel de
est égal au sous-groupe de
formé des
isométries laissant fixe
.
Démonstration
Soit
et
l'image par
de l'origine
. Ce point
est un point du réseau, donc le vecteur
appartient à
.
Soit
. Comme
et
laissent invariant
, il en est de même de
. De plus
, ce qui
démontre que
.
Fin de la démonstration
Cette proposition peut sembler évidente. Cependant, le fait que est un réseau joue un rôle important. Cela ne serait pas vrai pour n'importe quel ensemble à la place de .
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-2 Réseaux
→ II-2-5 Que signifie classifier ?
II-3 Classifions les pavages
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→ II-3 Classifions les pavages
Nous allons classifier les pavages selon l'équivalence suivante.
La symétrie de ne peut que diminuer par rapport à celle de :
On va donc énumérer les différentes possibiités selon le groupe
.
Définition
Deux pavages
et
sont équivalents s'il existe
une application affine
de
dans
telle que
La symétrie de ne peut que diminuer par rapport à celle de :
II-3-1 Le groupe ponctuel est contenu dans celui d'un réseau oblique
II-3-2 Le groupe ponctuel est contenu celui d'un réseau rectangle
II-3-3 Le groupe ponctuel est contenu dans le groupe du losange
II-3-4 Le groupe ponctuel est contenu dans le groupe du carré
II-3-5 Le groupe ponctuel est contenu dans le groupe du réseau hexagonal
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→ II-3 Classifions les pavages
II-3-1 Le groupe ponctuel est contenu dans celui d'un réseau oblique
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-3 Classifions les pavages
→ II-3-1 Le groupe ponctuel est contenu dans celui d'un réseau oblique
- p1
-
p2
contient une symétrie centrale pour un point . Prenons ce point pour origine.
Les éléments de sont de la forme avec ou 1. Le produit de deux éléments se calcule de la manière suivante
Invariants de symétrie : les centres de rotation (symétrie) forment un réseau homothétique de de rapport 1/2.
Les éléments qui ne sont pas des translations sont des symétries centrales par rapport à un point de .
DémonstrationSoient et deux points tels que et appartiennent à . Alors doit appartenir à . Comme , on a nécessairement . D'autre part, appartient à .
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-3 Classifions les pavages
→ II-3-1 Le groupe ponctuel est contenu dans celui d'un réseau oblique
II-3-2 Le groupe ponctuel est contenu celui d'un réseau rectangle
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-3 Classifions les pavages
→ II-3-2 Le groupe ponctuel est contenu celui d'un réseau rectangle
Prenons un rectangle de côté horizontal et de côté vertical . Le groupe est contenu dans le groupe du rectangle .
-
p1m
et il existe dans une réflexion axiale d'axe une droite de direction .
Le groupe est un sous-groupe de .
Les éléments de sont de la forme avec ou 1.
Le produit de deux éléments se calcule de la manière suivante
Les éléments de qui ne sont pas des translations sont toutes des réflexions d'axes de direction distants de multiples entiers de .
DémonstrationOn a les relations .
Fin de la démonstration
-
p1g
et il n'y a pas de réflexion axiale d'axe porté par dans . Par contre, il y a dans un élément de la forme pour une droite parallèle à et non entier. On a alorsce qui implique que est un entier. La droite est un axe de réflexion glissée.
Alors, appartient à pour tout entier . On a donc une infinité d'axes de glissage parallèles et distants d'un multiple entier de .
Les éléments de qui ne sont pas des translations sont des composés d'une symétrie par rapport à des axes de direction , c'est-à-dire d'une "symétrie-translation". Ces axes sont distants de multiples entiers de .
Dans les trois cas suivants, le groupe ponctuel est . La discussion va porter sur le fait qu'il y a ou non des symétries dans et sur la position du centre par rapport aux axes de symétrie ou de symétrie-translation. En effet, le composé d'une symétrie centrale et d'une translation est encore une symétrie centrale. Les réflexions ou se relèvent soient en des réflexions soit en des symétries glissées.
-
p2mm
et il existe une réflexion dans
avec de direction et un centre appartenant à .
Le composé est une réflexion d'axe la perpendiculaire à passant par .
L'ensemble est un sous-groupe de .
Le produit de deux éléments se calcule de la manière suivante . contient une infinité de réflexions d'axes de direction , équidistantes de multiples entiers de . Il existe aussi une infinité de réflexions d'axes parallèles à et elles sont équidistantes de multiples entiers de . Les centres de symétrie sont à l'intersection de ces axes de direction et .
-
p2mg
Il existe dans des réflexions par rapport à une droite de direction mais aucun centre de symétrie des symétries centrales qui sont dant ne se trouve sur une de ces droites .
Il n'y a pas de symétries par rapport à des droites de direction mais seulement des symétries glissées d'axe de glissage .
Le composé de par est une symétrie glissée où est la projection de sur .
La distance d'un axe de symétrie d'une réflexion ou d'un réflexion glissée à un centre de symétrie est un multiple impair de 1/4.
- p2gg
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-3 Classifions les pavages
→ II-3-2 Le groupe ponctuel est contenu celui d'un réseau rectangle
II-3-3 Le groupe ponctuel est contenu dans le groupe du losange
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-3 Classifions les pavages
→ II-3-3 Le groupe ponctuel est contenu dans le groupe du losange
Le losange est construit à partir de deux vecteurs
et
de
norme 1. Le groupe de symétrie du losange est d'ordre 4 formé de l'identité,
de la symétrie centrale par rapport au centre du losange et des symétries
par rapport aux deux diagonales :
.
Ce groupe a trois sous-groupes différents de lui-même. Le cas où
est d'ordre 1
ou est égal à
a déjà été traité.
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-3 Classifions les pavages
→ II-3-3 Le groupe ponctuel est contenu dans le groupe du losange
II-3-4 Le groupe ponctuel est contenu dans le groupe du carré
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-3 Classifions les pavages
→ II-3-4 Le groupe ponctuel est contenu dans le groupe du carré
Il est d'ordre 8. Il est composé de id, , , , , , , (réflexions par rapport aux médianes, ou diagonales).
Il possède trois sous-groupes distingués. Deux d'entre eux sont isomorphes à : et .
Le troisième est cyclique d'ordre 4 : .
Le cas où ne contient pas de rotation d'ordre 4 a été étudié dans le cas du rectangle.
-
p4
est le sous-groupe contenant les rotations d'angle . Le groupe de symétrie contient alors une rotation d'ordre 4. Les centres de rotation sont des centres de symétrie. Mais il y en a d'autres.
Dans les deux cas suivants, est le groupe du carré tout entier.
-
p4mm
et il existe une réflexion axiale dans dont l'axe passe par un centre de rotation. Le groupe de symétrie contient alors une rotation d'ordre 4. Il existe d'autre part toujours des réflexions (c'est un cas particulier du losange).
Les centres de symétrie sont alors les intersections des axes de réflexions, les intersections des axes de glissage, les centres de rotations.
- p4gm
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-3 Classifions les pavages
→ II-3-4 Le groupe ponctuel est contenu dans le groupe du carré
II-3-5 Le groupe ponctuel est contenu dans le groupe du réseau hexagonal
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-3 Classifions les pavages
→ II-3-5 Le groupe ponctuel est contenu dans le groupe du réseau hexagonal
Le réseau équilatéral est construit à partir des vecteurs et avec . L'angle entre et est donc de . C'est un cas particulier du réseau losange. Si est le centre de gravité de l'hexagone, Le groupe de symétrie du réseau équilatéral (ou hexagonal) est formé
- des rotations d'angle
,
,
 ,
,
,
,
- des réflexions par rapport aux diagonales (de direction et )
- des réflexions par rapport aux médianes (de direction et )
Géométrie du plan : Frises et Pavages
→
II Réseaux et pavages
→
II-3 Classifions les pavages
→ II-3-5 Le groupe ponctuel est contenu dans le groupe du réseau hexagonal
III D'autres groupes de symétrie
Géométrie du plan : Frises et Pavages
→ III D'autres groupes de symétrie
On connait des dessins ou des objets qui ont une "symétrie" qui n'est pas relié à la géométrie euclidienne du plan. C'est un autre type de groupes qui intervient alors.
Ce qui suit est inachevé ...


Pavage de Penrose
Géométrie du plan : Frises et Pavages
→ III D'autres groupes de symétrie
III-1 En spirale
Géométrie du plan : Frises et Pavages
→
III D'autres groupes de symétrie
→ III-1 En spirale
Exemple [Spirale]
Plaçons-nous dans le plan complexe où l'on a enlevé l'origine
. Soit
un nombre complexe non nul. L'application
est une bijection.
Soit
le groupe engendré par
dans
ou par
dans l'ensemble des applications bijectives de
dans lui-même.
Par exemple, si , c'est le sous-groupe de formé des nombres complexes

Par exemple, si , c'est le sous-groupe de formé des nombres complexes

Géométrie du plan : Frises et Pavages
→
III D'autres groupes de symétrie
→ III-1 En spirale
III-2 Plan hyperbolique
Géométrie du plan : Frises et Pavages
→
III D'autres groupes de symétrie
→ III-2 Plan hyperbolique
C'est le disque unité dans
. Les segments sont les arcs de cercles ou de droite
orthogonaux au bord (Poincaré, 1880). On part d'un polygone hyperbolique
convexe
dont les angles sont de la forme
où
est un
entier supérieur ou égal à 3. On suppose que
On construit les polygones symétriques de par rapport à chacun de ses côtés. On obtient ainsi de nouveaux polygones dont on reprend les symétriques par rapport à leurs côtés et ainsi de suite... Tous ces polygones forment un pavage périodique du plan hyperbolique.
Pavage du plan hyperbolique par des polygones
- soit les entiers sont pairs.
- soit les côtés de sont égaux.
On construit les polygones symétriques de par rapport à chacun de ses côtés. On obtient ainsi de nouveaux polygones dont on reprend les symétriques par rapport à leurs côtés et ainsi de suite... Tous ces polygones forment un pavage périodique du plan hyperbolique.
Pavage du plan hyperbolique par des polygones
Géométrie du plan : Frises et Pavages
→
III D'autres groupes de symétrie
→ III-2 Plan hyperbolique
 égal à 0 ou 1. La loi de groupe sur
est décrite par
égal à 0 ou 1. La loi de groupe sur
est décrite par
 égaux à 0 ou à 1.
égaux à 0 ou à 1.