Déterminer la loi de
| t |
|
|
|
Lois marginales et lois conditionnelles
On considère une variable aléatoire
à valeurs dans et une variable aléatoire
à valeurs dans . Le tableau ci-dessous donne la valeur de
pour
et
et donc caractérise la loi du couple
.
Par exemple,
et
= .
1. Déterminer la loi de .
1. Déterminer la loi de . Bonne réponse : la loi de est bien donnée par le tableau suivant :
2. Déterminer maintenant la loi .
Lois marginales
On considère une variable aléatoire
à valeurs dans et une variable aléatoire
à valeurs dans . Le tableau ci-dessous donne la valeur de
pour
et
et donc caractérise la loi du couple
.
Par exemple,
et
= .
Déterminer la loi de .
1. Déterminer la loi de . Bonne réponse : la loi de est bien donnée par le tableau suivant :
2. Déterminer maintenant la loi .
Evénement défini par deux v.a.
On considère une variable aléatoire
à valeurs dans et une variable aléatoire
à valeurs dans . Le tableau ci-dessous donne la valeur de
pour
et
et donc caractérise la loi du couple
.
Par exemple,
et
.
Calculer la probabilité de l'événement { }. P( ) =
.
Calcul d'une loi dépendant des deux v.a.
On considère deux variables aléatoires
et
à valeurs entières,
étant à valeurs dans et
étant à valeurs dans .
1. Déterminer les valeurs possibles pour la variable aléatoire
, c'est-à-dire les valeurs qui peuvent être prises avec une probabilité strictement positive (on séparera les valeurs par des virgules) :
.
Bonne réponse : les valeurs possibles pour
sont bien
.
Le tableau ci-dessous donne la valeur de
pour
et
et donc caractérise la loi du couple
.
Par exemple,
et
.
2. Déterminer la loi de la variable aléatoire
.
Covariance entre deux v.a.
On considère une variable aléatoire
à valeurs dans et une variable aléatoire
à valeurs dans . Le tableau ci-dessous donne la valeur de
pour
et
et donc caractérise la loi du couple
.
Par exemple,
et
.
Calculer :
. NB : la réponse peut être écrite sous forme d'une fraction ou sous forme décimale avec au moins 3 chiffres significatifs.
Indépendance de deux v.a.
On considère une variable aléatoire
à valeurs dans et une variable aléatoire
à valeurs dans . Le tableau ci-dessous donne la valeur de
pour
et
et donc caractérise la loi du couple
.
Par exemple,
et
.
Les variables
et
sont-elles indépendantes ?
.
Espérance conditionnelle
On considère deux variables aléatoires
et
à valeurs entières :
-
est à valeurs dans ;
-
est à valeurs dans .
Le tableau décrit la loi conditionnelle de
sachant {
} pour tout
{
} :
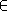 {
} :
{
} : Bonne réponse !
2. Le tableau ci-dessous décrit la loi de . Déterminer l'espérance de
Propriétés de la loi d'un couple de v.a.
Soit
et
deux variables aléatoires définies sur un espace de probabilité (
,
,
) à valeurs dans . - L'affirmation suivante est-elle toujours vraie ?
Si , alors
- L'affirmation suivante est-elle toujours vraie ?
Si , alors
Un exemple de couple de v.a.
On dispose d'un sac contenant boules blanches, boules noires et boules rouges indiscernables au toucher. On note
le nombre de boules blanches et
le nombre de boules noires que l'on obtient en tirant au hasard deux boules différentes.
Compléter le tableau en y mettant les valeurs de
pour
et
2, afin que le tableau décrive la loi du couple
|
| | 1 |
|
|
|
|---|
| 2 |
|
|
|
|---|
Par exemple, la case en bas à gauche doit contenir la valeur de
.
Séquence aléatoire I
Une source émet une suite de lettres choisies indépendamment les unes des autres parmi les lettres suivant la loi de probabilité suivante :
Quelle est la probabilité pour que, dans une telle suite, ?
Séquence aléatoire II
Une source émet une suite de lettres choisies indépendamment les unes des autres parmi les lettres suivant la loi de probabilité suivante :
- Quelle est la probabilité que, dans une telle suite, ?
Bonne réponse ! La probabilité que, dans une telle suite, est
- On vous dit que dans la suite de lettres émise par la source, . Quelle est la probabilité pour que, dans cette suite, ?
Sommation et couple de v.a. 1
Soit
un couple de variables aléatoires à valeurs entières. On considère l'ensemble
défini par
= {
tels que
et
}
Compléter l'expression ci-dessous de la probabilité de l'événement {
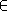 } :
} : |
| |
| |
|
|
| 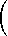 |
| 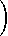 |
| | =
| | =
| |
Sommation et couple de v.a. 2
On considère un couple
de variables aléatoires à valeurs dans {1, ..., } x {1, ..., }. Compléter la formule ci-dessous afin d'exprimer la probabilité de l'événement A défini par : A : {
}, en fonction uniquement des probabilités
(
et
) pour
et
|
| | |
|
| 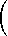 |
| 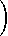 |
| |
| |
| |
NB : on écrira min(a,b) pour désigner le minimum entre deux réels a et b et max(a,b) pour désigner le maximum entre a et b. On n'utilisera pas de sommes de la forme
avec
.
Sommation et couple de v.a. 3
On considère un couple
de variables aléatoires à valeurs dans les entiers positifs ou nuls. L'objectif est d'exprimer la probabilité de l'événement {
}
uniquement à l'aide des probabilités
pour
et
.
- Pour cela, vous avez besoin d'une :
- Pour faire ce calcul,
on a besoin d'une .
on a besoin d'une .
on peut exprimer la probabilité de cet événement soit à l'aide d'une , soit à l'aide d'une .
- Complétez la formule ci-dessous :
|
| |
| |
|
|
| 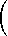 |
| 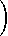 |
| | =
| | =
| |
NB : on écrira
- inf pour désigner
,
- max(a,b) pour désigner la maximum entre les réels a et b,
- min(a,b) pour désigner le minimum entre les réels a et b.
Tirage de deux numéros I
choisit au hasard un numéro entier entre 1 et . choisit au hasard un numéro entier entre 1 et . Notons
la variable aléatoire désignant le numéro tiré par et
la variable aléatoire désignant le numéro tiré par .
1- Compléter l'écriture suivante de l'événement A :
en utilisant les variables aléatoires
et
de la façon la plus simple possible : A : {
}
NB : on pourra utiliser les fonctions min, max et abs en mettant les arguments de ces fonctions entre parenthèses, séparés par une virgule s'il y en a deux. Par exemple, min(a,b) désigne le minimum entre les deux nombres a et b.
1- Compléter l'écriture suivante de l'événement A : ,
en utilisant les variables aléatoires
et
de la façon la plus simple possible. Bonne réponse ! l'événement
s'écrit : {
}
2- Calculer maintenant la probabilité pour que :
=
.
Tirage de deux numéros II
choisit au hasard un numéro entier entre 1 et . choisit au hasard un numéro entier entre 1 et .
- Calculer la probabilité pour que .
Bonne réponse ! la probabilité pour que est
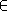 {
} :
{
} : 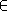 } :
} :