 such that the map
with
is bijective on the set of invertible elements of
. (You must take 10000
such that the map
with
is bijective on the set of invertible elements of
. (You must take 10000
 .)
.) Step 1. Find two prime numbers, and , such that , . Compute .
You have taken , , .
Step 2. Find an integer  such that the map
with
is bijective on the set of invertible elements of
. (You must take 10000
such that the map
with
is bijective on the set of invertible elements of
. (You must take 10000
 .)
.)
You have taken .
Step 3. Using
as the public key of an RSA cryptosystem, what is the private key, that is, the integer 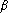 such that
?
such that
?
Suppose that in a secured communication, your partner has sent you a couple as the public key of an RSA cryptosystem, where
Now suppose that you have a message to sent to him. This (original) message is represented by the following number.
What is the corresponding crypted message that you should send? (The last number must be between 0 and N-1.)
We have two prime numbers, and . Let
Take such that the couple forms the public key of an RSA cryptosystem.
Step 1. Compute the prive key, that is, the integer 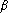 such that x
such that x 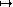 is the inverse of x
is the inverse of x 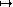 in
. (Among the choices of
in
. (Among the choices of 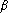 , you must take the smallest positive integer.)
, you must take the smallest positive integer.)
Yes, .
Step 2. Using the public key , your partner has sent you the following crypted message (number). What is the original message (number)? (This must be a number between 0 and N-1.)
You notice that the key is too short, so that you can decrypt the messages without knowledge of the private key, by using the online tools on WIMS. You are tempted to do so.
Step 1. Compute the privatge key, that is, the integer 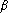 such that x
such that x 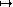 is the inverse of x
is the inverse of x 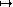 in
. (Among the choices of
in
. (Among the choices of 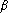 , you should take the smallest positive integer.)
, you should take the smallest positive integer.)
Yes, .
Step 2. Now you have intercepted the following crypted message (number). What is the original message (number)? (This must be a number between 0 and N-1.)
Please take note that WIMS pages are interactively generated; they are not ordinary HTML files. They must be used interactively ONLINE. It is useless for you to gather them through a robot program.