OEF subspace definition
--- Introduction ---
This module actually contains 21 exercises on the definition of
subspaces of vector spaces.
You are given a vector space and a subset defined in various ways;
up to you to determine whether the subset is a subspace.
See also the collections of exercises on
vector spaces in general or
defition of vector spaces.
Continuous functions
Let
be the
-vector space of real functions
, and let
be the subset of
composed of the function 0 and functions which are on [,].
Is
a subspace of
?
Increasing functions
Let
be the
-vector space of real functions
, and let
be the subset of
composed of the function 0 and functions which are on [,].
Is
a subspace of
?
Crossed Matrices
Let
be the vector space of matrices of size
, and let
be the subset of
composed of matrices
such that
Is
a subspace of
?
Matrices and determinant
Let
be the vector space of matrices of size ×, and let
be the subset of
composed of matrices M whose is equal to . Is
a subspace of
?
Matrices and elements
Let
be the vector space of matrices of size ×, and let
be the subset of
composed of matrices M such that . Is
a subspace of
?
Multiplied matrices
Let
be the vector space of matrices of size
, and let
be the subset of
composed of matrices
. Is
a subspace of
?
Matrices and rank
Let
be the vector space of matrices of size ×, and let
be the subset of
composed of matrices of rank . Is
a subspace of
?
You must give all the good replies.
Matrices with power
Let
be the vector space of matrices of size ×, and let
be the subset of
composed of matrices M such that M=0. Is
a subspace of
?
Periodic functions
Let
be the vector space of real continuous functions over
, and let
be the subset of
composed of the function 0 and periodic functions whose period . Is
a subspace of
?
Polynomials and coefficients
Let
be the
-vector space of real polynomials P(X) of degree less than or equal to , and let
be the subset of
composed of polynomials such that the of its coefficients equals . Is
a subspace of
?
Polynomials and degrees
Let
be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
with degree . Is
a subspace of
?
Polynomials and integral
Let
be the vector space over
of polynomials, and let
be the subset of
composed of polynomials
such that
Is
a subspace of
?
Polynomials and integral II
Let
be the vector space over
of polynomials, and let
be the subset of
composed of polynomials
such that
Is
a subspace of
?
Polynomials and roots
Let
be the
-vector space of real polynomials P(X) of degree less than or equal to , and let
be the subset of
composed of polynomials such that the of its roots (real or complex, counted with multiplicity) equals 0. Is
a subspace of
?
Polynomials and roots II
Let
be the
-vector space of real polynomials P(X) of degree less than or equal to , and let
be the subset of
composed of polynomials with . Is
a subspace of
?
Polynomials and values
Let
be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
such that
. Is
a subspace of
?
Polynomials and values II
Let
be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
(X) such that
. Is
a subspace of
?
Polynomials and values III
Let
=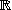 [X] be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
such that
.
[X] be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
such that
. Is
a subspace of
?
Real functions
Let
be the
-vector space of real functions
, and let
be the subset of
composed of functions
(x) .
Is
a subspace of
?
Square matrices
Let
be the vector space of matrices of size ×, and let
be the subset of
composed of matrices. Is
a subspace of
?
Vectors of R^3
Let
be the vector space of dimension 3 over
, and let
be the subset of
composed of vectors
such that
. Is
a subspace of
?
The most recent version
This page is not in its usual appearance because WIMS is unable to recognize your
web browser.
Please take note that WIMS pages are interactively generated; they are not ordinary
HTML files. They must be used interactively ONLINE. It is useless
for you to gather them through a robot program.
- Description: collection of exercices on the definition of subspace of vector spaces. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, algebra, linear algebra, vector space, subspace, polynomial, matrix, function
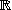 [X] be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
such that
.
[X] be the vector space of polynomials over
, and let
be the subset of
composed of polynomials
such that
.