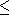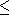OEF min-max2
--- Introduction ---
This module actually contains 12 exercises on the extrema of functions of two variables.
Distance from a point to a conic
What is the distance from the origin to the curve of equation
?
xrange -, + yrange -, + parallel -,0,+,0,0,1,40,grey parallel -,0,+,0,0,-1,40,grey parallel 0,-,0,+,1,0,40,grey parallel 0,-,0,+,-1,0,40,grey arrow 0,0, 0,1,10,black arrow 0,0, 1, 0 ,10,black vline 0,0, black hline 0,0, black levelcurve darkred, , levelcurve green,
This problem is interpreted as a constrained minima problem. Solve by by answering the following questions:
First: It is intended to find the minimum of the function of two variables
defined by
subject to the constraint
Second: With
and
we have grad
(
,
)
grad
(
,
)
These two vectors are related to point
if their determinant
is equal to
.
Third: Remember that grad
and grad
are parallel if
Give the value of the critical point
for which
is minumum on the curve
. A=(
,
)
The minimum distance of the curve at the point
is therefore equal to
The exercise has several steps
Distance from a point to a curve*
What is the distance from the origin to the curve of equation
?
xrange -, + yrange -, + parallel -,0,+,0,0,1,40,grey parallel -,0,+,0,0,-1,40,grey parallel 0,-,0,+,1,0,40,grey parallel 0,-,0,+,-1,0,40,grey arrow 0,0, 0,1,10,black arrow 0,0, 1, 0 ,10,black vline 0,0, black hline 0,0, black levelcurve darkred, , levelcurve green,
This problem is interpreted as a constrained minima problem. Solve by answering the following questions:
First: It is intended to find the minimum of the function of two variables
defined by
subject to the constraint
Second: With
and
, we have grad
(
,
)
grad
(
,
)
These two vectors are parallel in the point
if their determinant
is equal to
.
Third: Remember that grad
and grad
are parallel if
Give the value of the critical point
for which
is minumum on the curve
. A=(
,
)
The minimum distance of the curve at the point
is therefore equal to
Affine function on an ellipse
Find the point, subject to the constraints below, where the function
defined by
has its Constraints:
and
.
Extremum I
Let
be a function of two variables, from
to
of class
, and
a point in
. Assume that:
,
,
,
,
.
The point
is a critical point?
The point
is a
Extremum II
Let
a function from
to
defined by
.
The point
is a :
Critical point and level curves
Let
be a function of two variables, from
to
of class
, and
a point in
. Assume that in a neighbourdhood of a point
, we have:
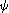
where 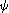 is a function of class
such that
is a function of class
such that 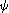 =0. Which of these three designs may represent the contours of
in a neighbourhood of
?
=0. Which of these three designs may represent the contours of
in a neighbourhood of
?
Maximum (with edges, pipe)
A pipe of trapezoidal profile is constructed by bending a plate of total width . Let
be the bend width at either side and
the angle that the bend portions make with the vertical (see drawing below). What are the values of
and
that maximize the pipe flow?
xrange -3.5, 3.5 yrange -3.5, 3.5 linewidth 3 arc 3.3, 3,3, 240,300, black lines green ,-3,1,-2,-1, 2,-1,3,1 line -3,1,3,1, red fill 0,0, skyblue transparent red
xrange -4.5, 4.5 yrange -4.5, 4.5 line -2,-1,-2,1,black text black,-3,1, medium, y text black,-3.5,0, medium, x arc -2,-1,2,2, 90,130, black linewidth 3 lines green ,-4,1,-2,-1, 2,-1,4,1
Solve by answering the following steps:
First: The surface we want to maximize is defined by the function
given by
on a domain
defined by
 x
x 
 y
y 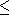
Second: Calculate the critical point of
which is within the domain
,
) and the
function value in this point :
For your information, here are the level curves of
xrange -0.5, yrange -0.5, parallel -1,0,,0,0,1,40,grey parallel -1,0,,0,0,-1,40,grey parallel 0,-1,0,,1,0,40,grey parallel 0,-1,0,,-1,0,40,grey levelcurve darkred, , vline 0,0, black hline 0,0, black linewidth 3 lines green, 0,0,0,pi/2, /2,pi/2, /2,0,0,0 linewidth 1 arrow 0,0, 0,1,10,black arrow 0,0, 1, 0 ,10,black disk ,, 5,blue
Third: Now compute what the maximum of
is, if
are taken on the edge of
Fourth: So, as a conclusion, the maximun flow is obtained for a value of
and a value of the angle (in radians)
Extremum on an area
We want to find the global of the function
defined by
over the closed triangular region
with vertices
,
and
. Do it by the following questions :
First: How many critical points are in the interior of
?
- Second: fill in the coordenates of the critical point
- Calculate the value of the function
at this point :
- Is the problem finished, without any further calculations ?
Third: We have
.
- What is the value of the function on the edge
(A and B included in the edge)?
- What is the value of the function on the edge
(B and C included in the edge)?
- What is the value of the function on the edge
(C and A included in the edge)?
- What is the value of the function on
xrange , yrange , fpoly grey,,, text black, , medium, A text black, , medium,B text black, , medium,C
Maximum volume with Conditions I
Calculate the volume of the largest rectangular parallelepiped - with a vertex in
,
- whose edges are parallel to the coordinate axes,
- which is in the first octant (nonnegative coordinates),
- The vertex opposite to
is in the plane of equation
Solve the problem by answering the following questions:
First: calculate the volum as a function
of
.
Second: The domain
of the function
given by
corresponding to this problem is a triangle
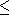
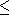 ,
,
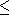
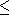
Third: How many critical points of the function
given by
are inside
Fourth: The critical point of
inside
is (
,
).
Fifth: The function
is zero at the edges of
. As the function
has a maximum, and the function values are positive inside and zero at the edges, the critical point
is necessarily a maximum. Calculate the lenghts
,
and
of three sides corresponding to the box of maximum volume, and the volume.
>
Maximum volume with conditions II
We want to find what the maximum possible volume of a rectangular box without top, made with
of cardboard, is Solve by answering the following questions
This problem is interpreted as a constrained maxima problem.
It is intended to find the maximum of the function of three variables
defined by
subject to the constraint
With
and
we have grad
(
,
,
)
grad
(
,
,
)
These two vectors are parallel in the point
if the vector product (
,
,
)
is equal to
.
The
value (giving the volume) for a point, with one zero coordenate, is equal to
. And the point
a maximum.
Thus, grad
and grad
are linearly dependent if
There is only one critical point for this problem such that all its coordinates are non-zero, this is the point
(
,
,
)
and the corresponding volume is
Least squares method
We have some evidences that the two quantities
and
are related by an affine relationship
. The experimental data give the following points
y=
x +
xrange -1,+1 yrange -1,+1 hline black, 0,0 vline black, 0,0 arrow 0,0,0,1,10,black arrow 0,0,1,0,10,black plot red , ()*x+()
Distance to the tangents of a conic
Calculate the point of the conic section
of equation
whose tangent to
is at the largest distance to the point
.
The most recent version
This page is not in its usual appearance because WIMS is unable to recognize your
web browser.
Please take note that WIMS pages are interactively generated; they are not ordinary
HTML files. They must be used interactively ONLINE. It is useless
for you to gather them through a robot program.
- Description: collection of exercises on the extrema of functions of two variables. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, analysis, maximum, minimum, extremum, point critique, maxima, minima
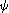
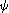
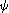 is a function of class
such that
is a function of class
such that 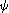 =0. Which of these three designs may represent the contours of
in a neighbourhood of
?
=0. Which of these three designs may represent the contours of
in a neighbourhood of
? 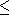 x
x 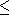
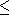 y
y 
 ,
,