Nombres complexes II
Objectifs
Documents
Voici les documents où vous pourrez travailler le cours.- F. Liret et D. Martinais, Mathématiques pour le DEUG, Algèbre 1ère Année (Dunod), chapitre 2
- A. Denmat et F. Héaulme, Algèbre générale (Dunod), TD 3 et 5
Guide
Histoire
d'Alembert
est le premier à avoir énoncé, sous une forme complète, le théorème fondamental de l'algèbre, souvent nommé simplement de d'Alembert, déjà avancé par Viète et Girard mais qu'ils n'arrivèrent pas à démontrer de façon précise :
Tout polynôme d'une variable complexe, de degré
, admet
racines complexes (éventuellement égales).
(Tiré de ChronoMath )
Equations dans les nombres complexes
- Racines carrées d'un nombre complexe
- Equation du second degré dans C
- Exercices sur les racines d'une équation de degré 2
- Racines cubiques et plus
- Exercice
Racines carrées d'un nombre complexe
Exercice :
Racine carrée
On désire trouver la racine carrée d'un nombre complexe donné de manière algébrique, par exemple
. On cherche donc un nombre complexe
tel que
avec
et
appartenant à  .
.
- On écrit ce que signifie l'équation
en termes de
et de
.
Comme , l'équation est équivalente au système d'équationsOn peut a priori résoudre à partir de ces deux équations. Mais on va en utiliser une autre qui va simplifier la résolution
- On traduit donc le fait que
ce qui donne
-
Et quand on a la valeur de
et celle de
, que
voulez-vous faire d'autre que d'en déduire la valeur de
et de
en ajoutant et retranchant ces deux équations :
Au fait, voyez-vous une raison a priori pour que ces valeurs soient positives ?
-
Donc,
et
Mais cela ferait 4 solutions !
Ce qui en fait vraiment beaucoup trop, puisque l'équation a deux solutions.
- Cela vient du fait que l'on n'a pas raisonné par conditions équivalentes. Quelle condition n'a-t-on pas utilisée ?
. Ainsi
et
sont de signe contraire.
Donc les solutions sont
et en approchant et .
Equation du second degré dans C
La résolution des équations du second degré est maintenant très simple, une fois que l'on sait trouver les racines carrées d'un nombre complexe. Par exemple, résolvons l'équation
Le discriminant est
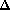 =
. On
calcule les racines carrées
de
=
. On
calcule les racines carrées
de 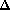 par la méthode précédente :
ou
.
Les racines de l'équation sont alors
par la méthode précédente :
ou
.
Les racines de l'équation sont alors
En particulier, comme dans le cas réel, l'équation a une racine "double" lorsque le discriminant
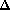 est nul.
est nul.
Exercices sur les racines d'une équation de degré 2
Exercice :
Racines d'un polynôme quadratique
Exercices sur les
racines doubles
Racines et coefficients
Il est important de connaître la relation entre les racines d'une équation de degré 2 et ses racines :
Si
u et
v sont les racines de l'équation
a x2 + b x + c=0 avec
a non nul, alors
Exercice :
lien entre racines et coefficients
Exercice :
Que peut-on dire de la différence des racines.
Exercices : Ici, vous devez trouver le polynôme de degré 2 dont les racines sont dessinées :
le polynôme à trouver est à
coefficients complexes
ou à
coefficients réels
Profitez-en pour remarquer comment sont placées les deux racines complexes d'un polynôme à coefficients réels
et faites le mélange suivant
coefficients réels ou complexes
Racines cubiques et plus
Exercice :
Placer les racines cubiques
dans le plan complexe.
Exercice :
Calculer les racines cubiques
Exercice : Placer les racines
quatrièmes
ou
cinquièmes
dans le plan complexe.
Exercice
Exercice :
Calculer les racines carrées de
. En
déduire les valeurs de
et .
Géométrie
Nombres complexes et géométrie
Exercice :
Résoudre dans
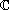 l'équation
z3 - u (1+i) z2+i u 2 z = 0 où
u est un nombre complexe donné non nul.
Montrer que les racines de cette équation sont les affixes des sommets
d'un triangle rectangle isocèle.
Aide
l'équation
z3 - u (1+i) z2+i u 2 z = 0 où
u est un nombre complexe donné non nul.
Montrer que les racines de cette équation sont les affixes des sommets
d'un triangle rectangle isocèle.
Aide
 l'équation
z3 - u (1+i) z2+i u 2 z = 0 où
u est un nombre complexe donné non nul.
Montrer que les racines de cette équation sont les affixes des sommets
d'un triangle rectangle isocèle.
Aide
l'équation
z3 - u (1+i) z2+i u 2 z = 0 où
u est un nombre complexe donné non nul.
Montrer que les racines de cette équation sont les affixes des sommets
d'un triangle rectangle isocèle.
Aide
Une des racines est facile à trouver :
c'est donc en fait une équation du second degré
que vous avez à résoudre !
Exercice :
Trouver l'ensemble des nombres complexes
z tels que les
points d'affixe
1, z et 1 + z2
soient alignés. Aide
Ecrire que
est réel.
Exercice :
triangle équilatéral et nombres complexes
Racines n-ièmes de l'unité
Voici les racines 6-ièmes de l'unité dans le plan complexe : avec , vous pouvez changer la valeur aléatoirement ou la choisir vous-même en haut (inférieure à 50).- Regarder les différences entre n pair et impair
- Essayer successivement des valeurs multiples, par exemple 2, 4, 12 ou 3, 6, 12, 24
n = 6
Racines de l'unité
Dans les exercices suivants, n'oubliez pas que si u est une racine de l'unité d'ordre n, par exemple,
elle vérifie la relation
Exercices sur les
racines cubiques de l'unité
et sur les
racines cinquièmes de l'unité
Exercices sur des
sommes de racines de l'unité
Pentagone
Exercice :
Dans le plan complexe, on considère le pentagone régulier
standard dont les sommets
sont les racines cinquièmes de l'unité
1, et .
-
Montrer que
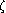 ,
,
et
sont
les racines du polynôme
X4+X3+X2+X+1.
,
,
et
sont
les racines du polynôme
X4+X3+X2+X+1.
Utiliser l'identité : X^5 - 1=(X-1)(X^4 + X^3 + X^2 + X + 1) - On pose
et
. Montrer que
 et
et
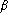 sont les racines du polynôme
X2 + X - 1. En déduire
les valeurs de
et
.
sont les racines du polynôme
X2 + X - 1. En déduire
les valeurs de
et
.
Calculer la somme \alpha + \beta et le produit \alpha \beta à l'aide de la question 1 . -
On trace le cercle
C de centre
passant par le point
.
Montrer que
C coupe l'axe des réels aux points
et
.
En déduire une construction du pentagone
régulier
à la règle et au compas. Faites-la avec le module
Règles et compas
et
proposez votre solution dans le forum si vous participez à une classe
(vous pouvez dans ce module sauver le script que vous aurez fait ).
Ecrire l'équation de C en terme d'affixes.