Déterminant
Guide
Le texte suivant introduit les déterminants en en donnant
une construction puis donne quelques propriétés.
On espère compléter ultérieurement la partie
déterminant et systèmes linéaires.
Déterminant des matrices
Définition de l'application déterminant
Soit
l'ensemble des matrices à coefficients dans un corps
(égal à
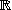
ou
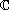
) ayant
lignes et
colonnes,
l'ensemble des matrices carrées d'ordre
à coefficients dans
. On note
-
la matrice identité d'ordre
-
où
est l'indice des lignes et
l'indice
des colonnes
-
ses
colonnes :
.
Théorème : Il existe une
unique application
, appelée
déterminant vérifiant les propriétés suivantes
-
pour tout
, pour tous
et
appartenant à
,
pour
et
des vecteurs colonnes,
+
.
-
s'il existe un indice
tel que
,
.
-
.
La propriété
est vraie même si les colonnes ne sont pas à côté l'une de l'autre, nous le démontrons à partir des propriétés telles qu'elles ont été énoncés ici :
s'il existe des indices
et
tels que
,
.
Conséquences immédiates de la définition
-
Echanger deux colonnes consécutives change le signe du déterminant.
Démonstration
d'après
.
=
=
+
+
d'après
,
=
d'après
.
Donc,
- S'il existe deux indices
et
différents tels que
,
Si deux colonnes sont égales ou proportionnelles, le déterminant est nul.
Démonstration
En échangeant successivement la
-ième colonne avec
sa voisine de manière à l'amener à la place
, on se retrouve dans
le cas où les deux colonnes égales sont côte à côte (d'après la
propriété précédente, le signe a peut-être changé).
- si
,
Echanger deux colonnes consécutives change le signe du déterminant.
Démonstration
On réapplique la même astuce que dans le premier cas, en utilisant
et en développant.
- si
On ne change pas le déterminant
en ajoutant à une colonne une combinaison linéaire des
autres colonnes.
Démonstration
+
d'après
,
d'après
.
- Si
où
est mis à la place de la
-ième colonne.
Démonstration
=
=
+...+
+...+
d'après
=
d'après
=
Petits cas
Pour
, on a nécessairement
.
Pour
, on a nécessairement
det
= det
=
det
+
det
=
det
+ c det
=
( det
+
det
)
+ c (det
+det
)
=
det
+
(
det
+ 0)
=
Développement par rapport à une colonne
Soit
la matrice extraite de
obtenue en enlevant la
-ième ligne
et la
-ième colonne. Alors,
Idée de la démonstration
Faisons la démonstration pour le développement par rapport à la première colonne.
On écrit
avec
le vecteur colonne formé de
sauf à la
-ième ligne
où il y a
. On a grâce à
Regardons le terme
.
Par exemple,
ici
En faisant des manipulations sur les colonnes du type
remplacer
par
, on obtient que
où
est la colonne
où on remplace le
-ième élément par
.
Exemple :
On remarque alors que l'application qui à une matrice
d'ordre
associe
avec
la matrice colonne obtenue à partir de
en rajoutant un
à la place
, vérifie les deux premières propriétés du déterminant
et vaut
sur l'identité
. Donc
.
Exemple :
Dans l'exemple ci-dessus, par rapport à quelle colonne a-t-on développé ?
=
Démonstration de l'existence et de l'unicité
Supposons par récurrence que l'existence et l'unicité de
det sont démontrés sur
avec
. La fonction déterminant sur
est notée en vert : det
Suposons l'existence de det sur
et montrons son
unicité.
-
Fixons deux entiers
et
. A une matrice
de
,
on attache la matrice
obtenue en rajoutant une colonne à la place
et une ligne à la place
formées de 0
sauf à leur intersection où l'on met 1 :
Par exemple
:
La fonction
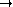 det
satisfait toutes les propriétés
pour le déterminant sur
et lui est donc
égale : pour et , faites-le ! le signe garantit la condition pour , car d'après , si on part de la matrice , après échanges de colonnes voisines, le coefficient arrive sur la diagonale et le signe est devenu 1.
det
satisfait toutes les propriétés
pour le déterminant sur
et lui est donc
égale : pour et , faites-le ! le signe garantit la condition pour , car d'après , si on part de la matrice , après échanges de colonnes voisines, le coefficient arrive sur la diagonale et le signe est devenu 1.
Le faire par exemple pour
Id(2,5)=
-
Par
et
(voir
conséquences immédiates
), det
) ne change pas si on met n'importe quel coefficient
à la
-ième ligne hors la
-ième colonne.
-
Si la fonction det existe pour
, on trouve par
la formule pour tout
indice de ligne
entre
1 et
:
det
det
.
où
est la matrice extraite, c'est-à-dire la matrice
privée de sa
-ième
ligne et de sa
-ième colonne.
Le membre de droite est fait avec des déterminants d'ordre
dont on sait qu'ils existent
et sont uniques par hypothèse de récurrence. Cela démontre l'unicité de det sur
.
Démontrons
l'existence de det sur .
Définissons une fonction sur
provisoirement appelée
deti par la formule
deti
det
.
(développement par rapport à la
-ième ligne) :
pour
:
=
+
+
Elle vérifie
:
justification
Soit
l'indice de la colonne où l'on a remplacé
par
et
la matrice extraite correspondant à la matrice
. Dans la somme définissant
deti
,
est remplacé par
et
ne change pas ; par contre
pour
différent de
,
ne change pas et
det
est remplacé par
det
+
det
en utilisant la propriété
pour
det.
Elle vérifie
:
justification
Soit l'indice
tel que les colonnes d'indice
et d'indice
soient égales.
Les matrices extraites
intervenant dans la formule
ont toutes deux colonnes égales et sont donc nulles
sauf les matrices extraites
et
qui sont égales :
deti
det
+
det
.
Elle vérifie
:
justification
deti
det
=1
L'unicité prouve de plus que les fonctions
deti ainsi définies
sont tous égales.
Matrice triangulaire
Si
est une matrice triangulaire inférieure, le déterminant de
est le produit de ses coefficients diagonaux
: on a
.
Démonstration
On raisonne par récurrence. On développe par rapport à
la première colonne si la matrice est triangulaire supérieure et par
rapport à la dernière colonne si la matrice est triangulaire inférieure.
Exemple : Le déterminant de
est égal à fois le déterminant de
.
Par récurrence, il vaut



Matrice inversible et déterminant
Théorème : Le déterminant
d'une matrice carrée
d'ordre
est nul si et seulement si le
rang de
est strictement inférieur à
, c'est-à-dire si et
seulement si
n'est pas inversible.
Démonstration :
- Si
, un des vecteurs-colonne de
est
combinaison linéaire des
autres. Donc
.
- Si
, alors
est inversible, on se ramène par des manipulations de colonnes
(par la méthode des pivots) à une matrice triangulaire dont les
éléments diagonaux sont tous non nuls. A chaque transformation,
le déterminant est multiplié par un scalaire non nul.
Donc,
.
Ainsi,
Théorème : Pour que
vecteurs d'un espace vectoriel de dimension
forment une base, il
faut et il suffit que le déterminant de la matrice formée avec leurs
composantes dans une base quelconque soit non nul.
La valeur absolue du déterminant d'une base a une interprétation
géométrique si l'on utilise le produit scalaire naturels de l'espace
vectoriel
comme volume du parallépipède construit à partir de la
base.
Multiplicativité
Théorème : Si
et
sont deux matrices carrées d'ordre
;
.
En particulier, si
est inversible,
Démonstration :
Si
n'est pas inversible,
ne l'est pas non plus et on a bien
.
Si
est inversible,
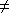
0. L'application
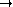
définie par
vérifie
toutes les propriétés du théorème-définition (exercice).
Par unicité, on a donc
.
Transposition
Théorème :
Si
est la
transposée
La transposée de la matrice
est la matrice
.
Par exemple, la transposée de
est la matrice
.
de la matrice
,
On peut ainsi développer le déterminant par rapport à une ligne et les propriétés du
théorème-définition restent vraies si on remplace les colonnes par les lignes.
Exercices
Exercice :
Des questions auxquelles il faut répondre très vite
Exercices :
-
Applications des règles de multilinéarité
-
Applications des règles de permutation
-
Applications de la multiplicativité
-
Produit
-
Calcul de déterminant I
-
Calcul de déterminant II
-
Calcul de déterminant "à la Gauss"
-
Déterminant paramétré
Déterminant paramétré
Exercice :
Déterminant et rang
Déterminant et vecteurs
Aire et déterminant
Théorème Dans le plan, l'aire du du parallélogramme formé à partir des
vecteurs
et
est égale à la valeur absolue du déterminant
de
et
Démonstration
L'aire du parallélogramme construit sur les deux vecteurs
et
est égale à |
| : calculons l'aire de la moitié de ce parallélogramme qui
est un triangle
.
Rappelons que l'aire d'un triangle ne change pas lorsqu'un des sommets se déplace
sur une parallèle au côté opposé :
Il ne reste plus qu'à découper le triangle
en trois triangles
et à déformer chacun d'entre eux sans en changer l'aire jusqu'à obtenir
une figure remplissant la moitié d'un rectangle de côtés de longueur
et
(et donc d'aire
) auquel on a enlevé un rectangle de côtés de longueur
et
donc d'aire
.
Magique !
Théorème :
L'aire du parallélogramme formé à partir des
vecteurs
et
est égale à la norme du produit
vectoriel de
et de
.
Démonstration
:
|
| Plaçons-nous dans le plan contenant les deux vecteurs
et
.
L'aire
à calculer est égale au produit de la longueur
du vecteur
et de la longueur
de la hauteur
correspondante. Le vecteur
associé à cette hauteur
est la projection de
sur la droite perpendiculaire à
.
Si
est le vecteur normal à
de même norme, on a donc
|
Théorème :
Le volume du parallélépipède formé à partir des
vecteurs
,
et
de
est égal à la valeur absolue du déterminant de
et de
et
calculée dans une base orthonormée.
Démonstration :
Le volume
est égal au produit de l'aire
du parallélogramme formé
par les vecteurs
et
et de la longueur
de la hauteur du parallélépipède
correspondante. Cette hauteur est par définition perpendiculaire au plan engendré par les vecteurs
et
. Si
est le vecteur représentant cette hauteur, il est donc
colinéaire à
et c'est la projection du vecteur
sur la droite engendrée par
.
Ainsi, on a
A =
Déterminant et vecteurs
Soit
un espace vectoriel de dimension
et
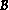
une base.
Définition :
Soit
vecteurs. On appelle déterminant de
dans la base
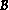
le déterminant
de la matrice des composantes des
dans la base
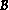
.
On le note
.
Proposition :
Le déterminant de
vecteurs dans une base dépend de la base :
Si
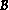
' est une autre base, si
est la matrice de passage
de
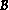
à
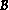
', on a
Produit mixte
Considérons un espace vectoriel
de dimension
muni d'un produit scalaire. Choisissons
une base orthonormée.
Soit
muni du produit scalaire
où
,
. Dans ce cas, la base canonique
est orthonormée, c'est-à-dire vérifie
si
et 0 sinon.
Théorème : Le déterminant de la matrice de passage
d'une base orthonormée à une autre base orthonormée
est égale à
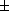
1 .
Démonstration : la matrice de passage
vérifie
. Donc on a
.
Une fois choisie une base orthonormée
,
le déterminant sépare les bases orthonormées en deux sous-ensembles :
- celles telles
que le
déterminant de la matrice de passage de
est égal à 1 (on les
appelle base orthonormée directe)
- celles dont le déterminant de la matrice de passage de
est égale à -1 (on les
appelle base orthonormée indirecte).
Définition : Soit
un espace vectoriel
de dimension
muni d'un produit scalaire (euclidien) et d'une base orthonormée
de référence.
On appelle produit mixte de
vecteurs
(on note aussi
) le déterminant de
dans la base
ou ce qui revient au même dans toute base orthonormée directe.
Produit vectoriel
Soit un espace vectoriel
de dimension
muni d'un produit scalaire et d'une base orthonormée
.
Définition : Soit
vecteurs
.
On appelle
produit vectoriel de
l'unique vecteur
noté
tel que
pour tout vecteur
de
.
Un tel vecteur existe grâce au théorème suivant :
Théorème : Soit un espace vectoriel
de dimension
muni d'un produit scalaire.
Soit
une forme linéaire de
dans
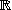
. Alors,
il existe une unique vecteur
dans
tel que
.
Exemple : Prenons
:
le produit vectoriel de
est le vecteur déduit de
par une rotation
d'angle
: on doit en effet avoir
.
Si les composantes de
,
et
dans la base
sont respectivement
,
et
, on doit avoir
pour tous
et
dans
.
Donc les composantes de
sont
.
Produit vectoriel : propriétés
Les propriétés suivantes se déduisent de la définition
et des propriétés du déterminant :
-
Soit
un entier entre 1 et
. L'application
est linéaire :
Définition : On dit que
est une
forme -linéaire.
-
Définition : On dit que
est une
forme -linéaire alternée.
-
est perpendiculaire à chacun des vecteurs
Démonstration :
ce qui est nul par la propriété
du déterminant
- Le calcul des composantes du produit vectoriel de deux vecteurs en dimension 3 est
une conséquence de la formule de développement par rapport à la dernière colonne :
Si
est de composantes
dans la base
et si
est la matrice des vecteurs colonnes de
dans la base
,
on a
où
la matrice obtenue à partir de
en enlevant la
-ième ligne.
- Si les vecteurs
sont linéairement indépendants,
est non nul et la famille de vecteurs
forment une base
directe : le déterminant de ces vecteurs dans la base est strictement positif
.
On utilise aussi les déterminants dans le cas de systèmes linéaires qui ne sont
pas de Cramer.
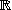 ou
ou
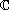 ) ayant
lignes et
colonnes,
l'ensemble des matrices carrées d'ordre
à coefficients dans
. On note
) ayant
lignes et
colonnes,
l'ensemble des matrices carrées d'ordre
à coefficients dans
. On note 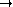 det
satisfait toutes les propriétés
pour le déterminant sur
et lui est donc
égale : pour et , faites-le ! le signe garantit la condition pour , car d'après , si on part de la matrice , après échanges de colonnes voisines, le coefficient arrive sur la diagonale et le signe est devenu 1. Le faire par exemple pour
det
satisfait toutes les propriétés
pour le déterminant sur
et lui est donc
égale : pour et , faites-le ! le signe garantit la condition pour , car d'après , si on part de la matrice , après échanges de colonnes voisines, le coefficient arrive sur la diagonale et le signe est devenu 1. Le faire par exemple pour


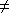 0. L'application
0. L'application
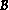 une base.
une base.
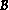 le déterminant
de la matrice des composantes des
dans la base
le déterminant
de la matrice des composantes des
dans la base 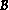 .
On le note
.
.
On le note
.
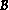 ' est une autre base, si
est la matrice de passage
de
' est une autre base, si
est la matrice de passage
de 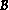 à
à 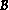 ', on a
', on a
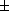 1 .
1 .
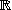 . Alors,
il existe une unique vecteur
dans
tel que
.
. Alors,
il existe une unique vecteur
dans
tel que
.