Longueur et intégrale curviligne
Objectifs
Documents
- F. Liret et D. Martinais, Mathématiques pour le DEUG, Analyse 2ième Année (Dunod).
- J. Stewart, Analyse, concepts et contextes, vol. 2, DeBoeck Université (2001)
Guide
- Longueur d'une courbe paramétrée
- Abscisse curviligne
- Intégrale curviligne d'une fonction
- Utilisation en physique
Longueur d'une courbe paramétrée
- Longueur d'une courbe paramétrée
- Le segment
- Dessin de lignes polygonales
- Exemple
- Une courbe et plusieurs paramétrages
- Propriétés simples de la longueur
- Formule pour la longueur
- Démonstration
- Calculs en coordonnées polaires
Longueur d'une courbe paramétrée
Exemple du segment La longueur d'un segment paramétré par
,
pour
est égale à
où
est le vecteur dérivé de la paramétrisation choisie du segment.
)
où
est le vecteur
. Le vecteur
est aussi le vecteur
dérivé de la fonction
. Ainsi,
la longueur du segment s'écrit aussi
En général
Soit une courbe paramétrée : , pour . Prenons une subdivision de l'intervalle [ ] en parties :
.
Soit la ligne polygonale passant par les points de la courbe et notons la longueur de cette courbe.
Définition :
On appelle longueur de la courbe
la borne supérieure
si elle existe des longueurs
des lignes
polygonales inscrites
.
Dessin
.
.
.
.
.
.
Dans le dessin,
- le paramètre parcourt la ligne verte qui est subdivisée en parties. Il est lié par un fil vert pointillé au point vert de la courbe ;
- La ligne polygonale est tracée en rouge et la courbe en bleu.
Exemple
|
. . |
Dans le dessin,
|
Une courbe et plusieurs paramétrages
Ici, ont été tracées des courbes paramétrées de paramètres , , , dont la représentation graphique est la même mais avec des paramétrages différents. . . . . .
Les changements de paramétrage sont donnés en fonction du premier par
,
,
,
Propriétés simples de la longueur
- Dans le cas d'un segment, la définition qu'on vient de donner donne la longueur du segment usuelle
-
Si
est la restriction de
 à un intervalle de
,
à un intervalle de
,
-
Si l'on met bout à bout deux arcs
 et
, la longueur de l'arc obtenu
est la somme des longueurs des arcs
et
, la longueur de l'arc obtenu
est la somme des longueurs des arcs
 et
et
Formule pour la longueur
Proposition :
Si
est une courbe
C1, sa longueur existe et on a
ou en notant
le vecteur vitesse,
Exercices :
- Chemin en montagne
- Longueur et projection
Démonstration
Formule pour la longueur
Preuve
Proposition :
Si
est une courbe
C1, sa longueur existe et on a
ou en notant
le vecteur vitesse,
Exercices :
Redémontrons analytiquement l'inégalité que - Chemin en montagne
- Longueur et projection
.
Preuve
On a
Le premier terme est la longueur du segment , en faisant la somme sur i, on obtient
.
Donc, par l'inégalité triangulaire,
Le premier terme est la longueur du segment , en faisant la somme sur i, on obtient
En particulier, l'ensemble des longueurs de lignes polygonales inscrites est un ensemble borné dont un majorant est .
La longueur existe à cause de la
propriété fondamentale des réels
Toute partie majorée non vide de
 admet une borne supérieure.
admet une borne supérieure.
 admet une borne supérieure.
admet une borne supérieure.
Pour
t 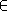 [a,b], soit
la restriction de
[a,b], soit
la restriction de
 à
. Notons
L(t) la longueur de
.
Nous allons montrer que
L est dérivable et de dérivée
, ce qui prouvera la
proposition.
à
. Notons
L(t) la longueur de
.
Nous allons montrer que
L est dérivable et de dérivée
, ce qui prouvera la
proposition.
Preuve
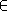 [a,b], soit
la restriction de
[a,b], soit
la restriction de
 à
. Notons
L(t) la longueur de
.
Nous allons montrer que
L est dérivable et de dérivée
, ce qui prouvera la
proposition.
à
. Notons
L(t) la longueur de
.
Nous allons montrer que
L est dérivable et de dérivée
, ce qui prouvera la
proposition.
Proposition :
Si
est une courbe
C1, sa longueur existe et on a
ou en notant
le vecteur vitesse,
Exercices :
- Chemin en montagne
- Longueur et projection
Preuve
Si
Mt et
Mt+h sont les points
et
,
L(t+h)-L(t) est la longueur de l'arc qui joint
Mt et
Mt+h. On a alors un encadrement de cette longueur
Comme les deux membres extrêmes ont pour limite
|| '(t)|| quand
h tend vers 0,
on obtient bien que
L est dérivable et de dérivée
.
'(t)|| quand
h tend vers 0,
on obtient bien que
L est dérivable et de dérivée
.
 '(t)|| quand
h tend vers 0,
on obtient bien que
L est dérivable et de dérivée
.
'(t)|| quand
h tend vers 0,
on obtient bien que
L est dérivable et de dérivée
.
Calculs en coordonnées polaires
Soit une courbe donnée en coordonnées polaires
par
pour
. En prenant
donnée en coordonnées polaires
par
pour
. En prenant
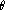 comme paramètre, un paramétrage de
C est donnée par
comme paramètre, un paramétrage de
C est donnée par
,
sa norme vaut
et on obtient la formule
Exercices :
- Longueur d'une courbe en coordonnées polaires
Abscisse curviligne
Définition : Un paramétrage d'une courbe
est une abscisse curviligne
si le vecteur vitesse relatif à cette paramétrisation est unitaire.
Ainsi, la courbe est paramétrée par un paramètre s, d'équations et on a f'(s)2+g'(s)2=1.
On dit alors que la courbe est paramétrée par son abscisse curviligne .
L'abscisse curviligne est aussi, à une constante près et au signe près, la longueur de la courbe d'un point fixé au point de paramètre s :
Propriété : Si
s est une abscisse curviligne de la courbe paramétrée, la longueur de l'arc de courbe comprise entre
le point de paramètre
s et le point de paramètre
s0 est égale à la valeur absolue de
s-s0.
On doit donc avoir :
Exemple du cercle
Exemple : La mesure de l'angle
au centre sur un cercle (en radian) est une abscisse curviligne du cercle.
Cela signifie que la longueur de l'arc de cercle de rayon 1 correspondant
à un angle
u en radians est exactement
u :
Par contre, le paramétrage du cercle donné par
n'est pas une abscisse curviligne du cercle. La norme du vecteur dérivé est égale à
. La longueur de l'arc de cercle compris entre les points de paramètre 0 et
a est donnée par la formule
.
Intégrale curviligne d'une fonction
On partage l'intervalle [a,b] en n parties égales a=t0< ... <tn=b, soit Pi=(xi,yi)= (f(ti), g(ti)) le point de paramètre ti et on note la longueur du segment Pi-1 Pi. Définition :
Soit
C une courbe paramétrée et
F une fonction définie sur
C. L'intégrale curviligne de
F le long de
C est la limite si elle existe des
lorsque
.
On la note alors
.
On démontre comme pour la longueur le théorème suivant :
Théorème :
Si
F est une fonction continue, la limite précédente existe et vaut
.
Exercices :
- Intégrale curviligne d'une fonction formelle
- Intégrale curviligne d'une fonction le long d'une ligne polygonale
Utilisation en physique
L'interprétation physiques de l'intégrale curviligne d'une fonction le long d'une courbe dépend de l'interprétation de cette fonction. Voici quelques exemples :Masse et centre de masse, moments d'inertie
Supposons qu'un fil suive une courbe C et que la fonction d(x,y) en un point (x,y,z) de C représente sa densité linéique. SiLe centre de masse (centre de gravité) se trouve au point G de coordonnées (xG,yG) avec
Exercices
- Masse en dimension 2
- Masse en dimension 3