Commençons par des exemples
arithmétiques ou
numériques :
relatifs, réels ou rationnels :
I-2-1-1 Les nombres
Soit
l'ensemble des nombres relatifs ou
l'ensemble des nombres rationnels
ou
l'ensemble des nombres réels. Pour tous éléments
,
,
de
-
;
-
;
-
;
- il existe un élément
tel que
.
I-2-1-2 Les racines de l'unité
Soit n un entier
. Soit
l'ensemble des nombres complexes
pour
. C'est aussi l'ensemble des nombres complexes
vérifiant
.
Il vérifie pour
dans
et
et
enties
-
;
-
;
-
;
-
.
Autrement dit, pour tous éléments
,
,
de
-
;
-
;
-
;
- il existe un élément
tel que
.
Exercice
Dessiner
,
,
,
... Pour
,
prendre
et repérer successivement les produits
pour
:
,
,
, ...
Exercice
Racines de l'unité et puissances
Sous-groupe de racines de l'unité
Sous-groupe de racines de l'unité II
Sous-groupe de racines de l'unité III
Des manipulations sur trois boules permettent aussi de trouver un groupe :
I-2-1-3 Permutations
(Lire la BD de Stewart : Ah les beaux
groupes - les chroniques de Rose Polymath (Belin) )
On a trois boules alignées. On peut ne pas changer leur ordre. C'est l'opération
identité
. On peut changer leur ordre en échangant les deux premières
(opération
), en faisant tourner les trois dernières (opération
) et en effectuant
ces opérations successivement. Donner
le résultat comme un tableau : si une opération nouvelle apparaît, lui donner un nom (
, ...) et la
rajouter.
|
|
|
|
|
|
|
| ... | |
|
| | | | | | | | | |
|
| | | | | | | | | |
|
| | | | | | | | | |
|
| | | | | | | | | |
|
| | | | | | | | | |
|
| | | | | | | | | |
|
| | | | | | | | | |
|
... | | | | | | | | | |
|
| | | | | | | | | |
On appelle ces opérations des
permutations
de l'ensemble des trois boules.
On note
la permutation qui transforme 1, 2, 3 en
,
,
. Par exemple,
est la permutation qui transforme 1, 2, 3 en 2, 3, 1.
Exercice
Permutations I
Permutations II
Permutations III
Enfin, voici un exemple de groupe formé d'applications.
I-2-1-4 Applications
Soient les applications suivantes définies sur
:
|
|
|
|
|
|
|
|
|
|
|
|
On peut composer ces applications ; donner le résultat comme un tableau :
si une application
nouvelle apparaît, lui donner un nom et la rajouter.
|
|
|
|
|
|
|
|
|
| | | | | | |
|
|
| | | | | | |
|
|
| | | | | | |
|
|
| | | | | | |
|
|
| | | | | | |
|
|
| | | | | | |
|
|
| | | | | | |
|
Pouvez-vous vous arrêter ?

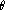 entre 0 et
). On pose
.
entre 0 et
). On pose
.
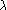 :
:
 tels que
et tels que
.
tels que
et tels que
.
 si
.
si
.
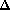 d'équation
dans le repère
.
d'équation
dans le repère
.